正準相関分析と固有値問題
正準相関分析がいかにして固有値問題へと帰着されるのかについて。
(PDFverはこちら)
目次
正準相関分析とは
一次元データ同士の相関は、次の図にあるように散布図としてプロットした場合にどれだけ一直線に並んでいるか、という「相関係数」の指標で評価出来ます。これは直感的にわかりやすく、数値計算も2データについての共分散と分散の値から簡単に計算出来ます。
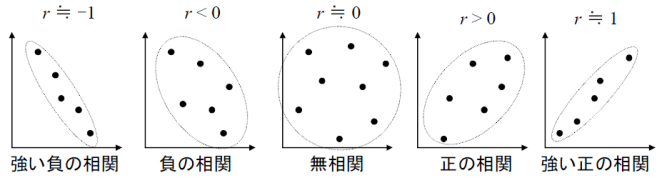
しかし、現実には2次元以上の多次元データが与えられる場合ももちろんあります。

さて、2次元以上の多次元データ同士がどれほど相関を持つか、をどのように判断すればよいでしょうか。ここで「正準相関分析」という手法が登場します。正準相関分析では多次元データを1次元に変換し、変換後の1次元データ同士について相関係数を求めます。この際、相関係数が最も大きくなるような変換方法を選ぶものとします。先日記事を書いた「主成分分析」においては、データの次元の削減を行い、その際削減後の分散が最大となる変換を選びました。正準相関分析もこれと非常に似ていると言えます。さらに共通する重大な特徴として、正準相関分析と主成分分析はともに固有値問題へと帰着されるということが挙げられます。以下では、具体的に正準相関分析の手法を詳しく見ていきます。
blog.aidemy.net
多次元データ
多次元データがN個あるとする。$\vec{X}^{(1)}、\vec{X}^{(2)} \cdot \cdot \cdot 、\vec{X}^{(N)} $と$\vec{Y}^{(1)}、\vec{Y}^{(2)} \cdot \cdot \cdot 、\vec{Y}^{(N)} $のようにN要素の列ベクトルで表す。
横に並べた行列を定義しておく。
\begin{eqnarray}
X &\equiv& \left( \begin{array}{cccc}
\vec{X}^{(1)} &\vec{X}^{(2)} & \cdot \cdot \cdot & \vec{X}^{(N)}
\end{array} \right)
\end{eqnarray} 2つに分けた多次元パラメーター同士の相関を見たい場合、それぞれの多次元パラメーターをスカラー量に変換し、N個のスカラー量データの相関を測れば良い。これが「正準相関分析」である。変換に用いる列ベクトルを$\vec{a}$として、
\begin{equation}
\vec{a}^\mathrm{T} X = \left( \begin{array}{cccc}
\vec{a}^\mathrm{T} \vec{X}^{(1)} &\vec{a}^\mathrm{T} \vec{X}^{(2)} & \cdot \cdot \cdot & \vec{a}^\mathrm{T} \vec{X}^{(N)}
\end{array} \right)
\end{equation} となる。各要素がスカラーである一次元のN点データとなっている。この変換に使う$\vec{a}$には最終的な相関が最大となるようなものを用いる。
相関係数
その相関の度合いを表す概念としては「相関係数」を用いる(cf 倉田著 入門統計解析p.72など)。2データ$x,y$の間の相関係数$\rho$は、共分散$S_{xy}$、標準偏差$S_x, S_y$、分散$\delta_x, \delta_y$などとすると、次のようになる。
\begin{eqnarray}
\rho &=& \frac{S_{xy}}{S_x S_y} \\
&=& \frac{S_{xy}}{\sqrt{\delta_x} \sqrt{\delta_y}} \\
&=& \frac{\vec{a}^\mathrm{T} V_{xy} \vec{b}} {\sqrt{\vec{a}^\mathrm{T} V_{xx} \vec{a}} \sqrt{\vec{b}^\mathrm{T} V_{yy} \vec{b}} }
\end{eqnarray}
Lagrangeの未定乗数法
相関係数$\rho$の表式は
\begin{eqnarray}
\rho &=& \frac{\vec{a}^\mathrm{T} V_{xy} \vec{b}} {\sqrt{\vec{a}^\mathrm{T} V_{xx} \vec{a}} \sqrt{\vec{b}^\mathrm{T} V_{yy} \vec{b}} }
\end{eqnarray} であった。これを最大にしたい。分子にある2項について、$\sqrt{\vec{a}^\mathrm{T} V_{xx} \vec{a}}=1, \sqrt{\vec{b}^\mathrm{T} V_{yy} \vec{b}} = 1$という条件を付けると、式がとても簡単になる。この条件下で$\rho$を最大化しよう($\vec a, \vec b$ は定数倍しても$\rho$は変化しないので制限を課しても問題ない)。Lagrangeの未定乗数法を用いる。
\begin{eqnarray}
L(\vec a, \vec b, \lambda_x, \lambda_y) &\equiv& \vec{a}^\mathrm{T} V_{xy} \vec{b} - \frac{\lambda_x}{2} (\vec{a}^\mathrm{T} V_{xx} \vec{a} -1) - \frac{\lambda_y}{2} (\vec{b}^\mathrm{T} V_{yy} \vec{b} - 1)
\end{eqnarray}として、偏微分を計算すると
\begin{eqnarray}
\frac{\partial L}{\partial \vec a} &=&
\left( \begin{array}{c}
\frac{\partial L}{\partial a_1} \\ \frac{\partial L}{\partial a_2} \\ \cdot \\ \cdot \\ \cdot \\ \frac{\partial L}{\partial a_N}
\end{array} \right) = V_{xy}\vec b - \lambda_x V_{xx} \vec{a} \\ \\
\frac{\partial L}{\partial \vec b} &=& V_{xy}^{\mathrm T} \vec a - \lambda_y V_{yy} \vec{b}
\end{eqnarray}
偏微分が0になることから、次の2式が導出される。
\begin{eqnarray} \left\{ \begin{array}{r@{\,}r@{\,}r}
V_{xy}\vec b - \lambda_x V_{xx} \vec{a} = 0 \\
V_{xy}^{\mathrm T} \vec a - \lambda_y V_{yy} \vec{b} = 0
\end{array} \right. \end{eqnarray} 第二式を変形して、
\begin{eqnarray}
\vec b = \frac{1}{\lambda_y} V_{yy}^{-1} V_{xy}^{\mathrm T} \vec a
\end{eqnarray} これを第一式に代入して、
\begin{eqnarray}
V_{xy} V_{yy}^{-1} V_{xy}^{\mathrm T} \vec a = \lambda_x \lambda_y V_{xx} \vec{a}
\end{eqnarray} 条件式は次の2式となった。
\begin{eqnarray} \left\{ \begin{array}{r@{\,}r@{\,}r}
V_{xy} V_{yy}^{-1} V_{xy}^{\mathrm T} \vec a &=& \lambda_x \lambda_y V_{xx} \vec{a} \\
\vec b &=& \frac{1}{\lambda_y} V_{yy}^{-1} V_{xy}^{\mathrm T} \vec a
\end{array} \right. \end{eqnarray}
Cholesky分解
Cholesky分解を行う。
\begin{eqnarray}
V_{xx} = L_{xx} L_{xx}^{\mathrm T}
\end{eqnarray} のように分解すると、
\begin{eqnarray}
V_{xy} V_{yy}^{-1} V_{xy}^{\mathrm T} \vec a &=& \lambda_x \lambda_y L_{xx} L_{xx}^{\mathrm T} \vec{a} \\
L_{xx}^{-1} V_{xy} V_{yy}^{-1} V_{xy}^{\mathrm T} (L_{xx}^{\mathrm T -1} L_{xx}^{\mathrm T}) \vec a &=& \lambda_x \lambda_y L_{xx}^{\mathrm T} \vec{a} \\
L_{xx}^{-1} V_{xy} V_{yy}^{-1} V_{xy}^{\mathrm T} L_{xx}^{\mathrm T -1} (L_{xx}^{\mathrm T} \vec a) &=& \lambda_x \lambda_y (L_{xx}^{\mathrm T} \vec{a})
\end{eqnarray} これで固有値問題へと帰着された!!
固有方程式を解くことで、$\vec a$が求まり、さらに「$\vec b = \frac{1}{\lambda_y} V_{yy}^{-1} V_{xy}^{\mathrm T} \vec a$」と「$\vec{b}^\mathrm{T} V_{yy} \vec{b} = 1$」を満たすような$\vec b$も求めることが出来る。$\vec a , \vec b$から、相関係数$\rho = \vec{a}^\mathrm{T} V_{xy} \vec{b} $が求まる。