新プログラミング言語「Q#」で量子テレポーテーション
Microsoftより前々から予告されていた、量子コンピューター向けの新プログラミング言語「Q#」及び開発キット「Quantum Development Kit」のプレビュー版が公開されました。
pc.watch.impress.co.jp
記事からの引用ですが、
(1)量子コンピューティング用のプログラミング言語「Q#」
(2)量子コンピューティングのシミュレーター(ローカルとAzure)
(3)量子コンピューティング向けコードのライブラリやサンプル
の3つが「Quantum Development Kit」には含まれています。
今回は、ローカル(Visual Studio)上において、Q#のコードを実装して量子計算のシミュレーションを行います。「準備編」および「Q#を書いてみよう」の内容は、公式HP(英語)に準拠して書いています(2017年12月15日時点)。
目次
準備編
Q#の開発環境を構築します。次の2つのソフトウェアのインストールが必要となります。
・「Visual Studio 2017」
・「Quantum Development Kit」 (今のところWindowsのみ対応)
「Visual Studio 2017」のインストール
こちらの公式サイトからダウンロードすることが出来ます。
www.visualstudio.com
Download for Windowsにカーソルを合わせ、Community 2017を選択するとダウンロード出来ます。
vs_community~から始まる名前の実行ファイルがダウンロードされているはずなので、これを実行しインストールします。インストールを進めていくと次の画面が表示されます。
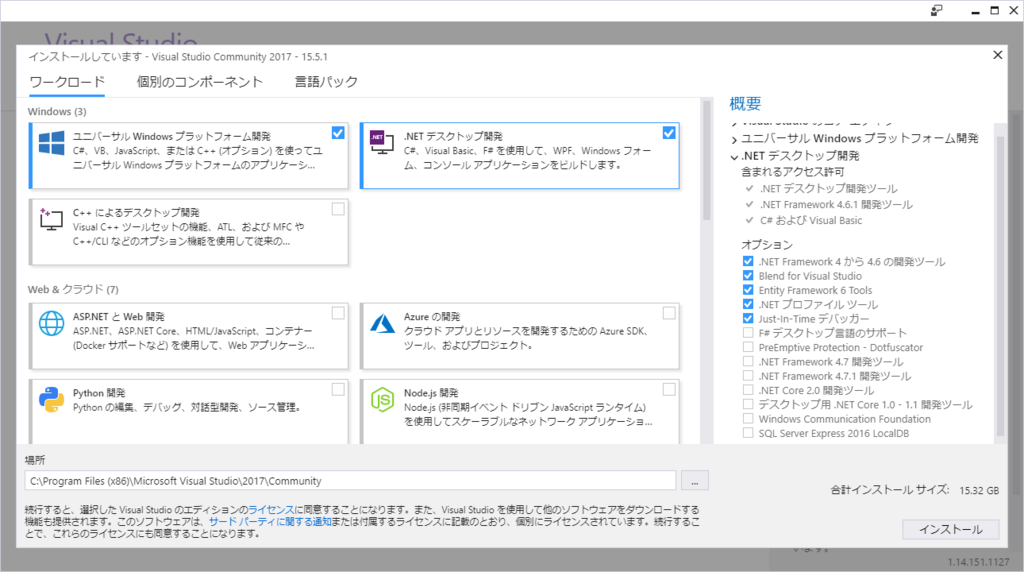
注意点として、「ユニバーサルWindowsプラットフォーム開発」と 「.NETデスクトップ開発」の2つの項目に必ずチェックを付けておきましょう。チェックを付けたら、右下のインストールをクリックします。インストールに成功すれば完了です。
「Quantum Development Kit」のインストール
こちらの公式HPに飛び、Download nowを選択。
次のページで名前や所属を入力し、Download nowボタンをクリックすると、次のページが表示されます。
ここでDownloadをクリックします。
QsharpVSIX.vsixというファイルがダウンロードされているはずなので、実行します。
Visual Studioが正しくインストールされていれば、.vsixがVisual Studioの拡張インストールパッケージであることが認識され、次のようなインストール画面が表示さあれます。
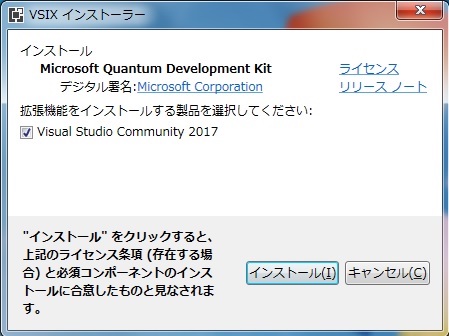
動作確認
Visual Studioを起動し、メニューバーのチーム>接続の管理をクリックします。画面右にチーム エクスプローラーが出現します。
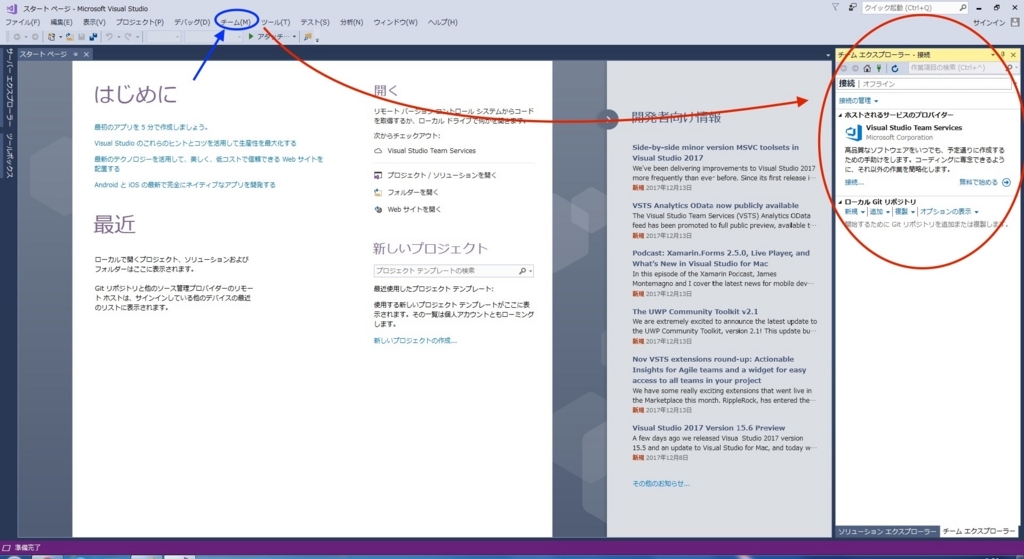
ローカルGitリポジトリの下の複製をクリックします。
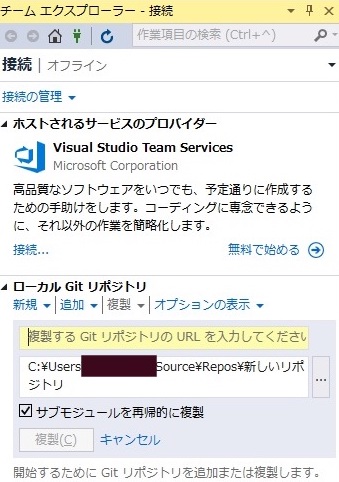
https://github.com/Microsoft/Quantum.gitと入力し、複製をクリックします。複製が終わると、チーム エクスプローラーがソリューションエクスプローラーに切り替わります。
切り替わったソリューションエクスプローラー内にある、QsharpLIbraries.slnをダブルクリックします。
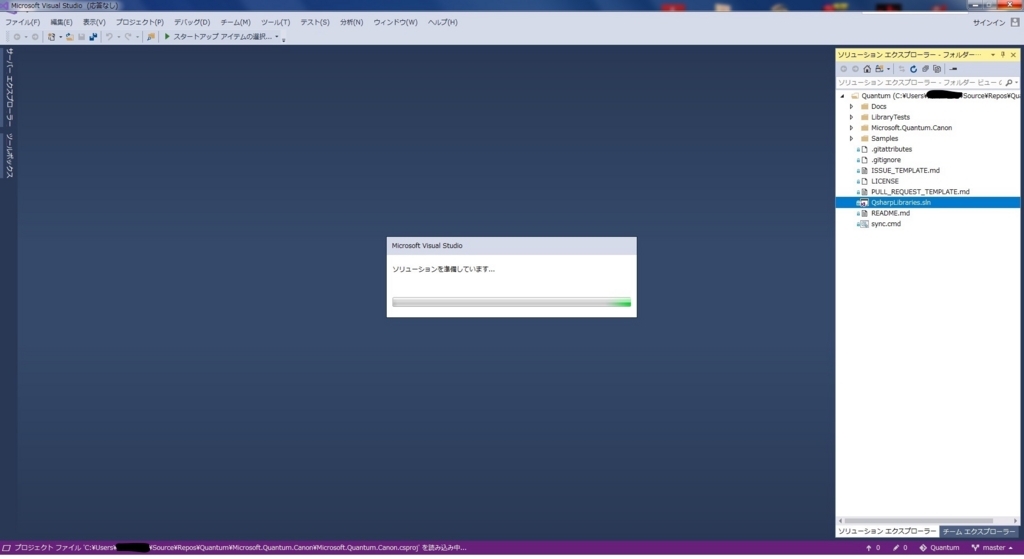
何らかのインストールが要求される場合があるので、指示に従ってインストールを行います。
次に、ソリューションエクスプローラー内のSamples > 0.Introduction > TeleportationSampleを右クリック、スタートアッププロジェクトに設定を左クリックします。
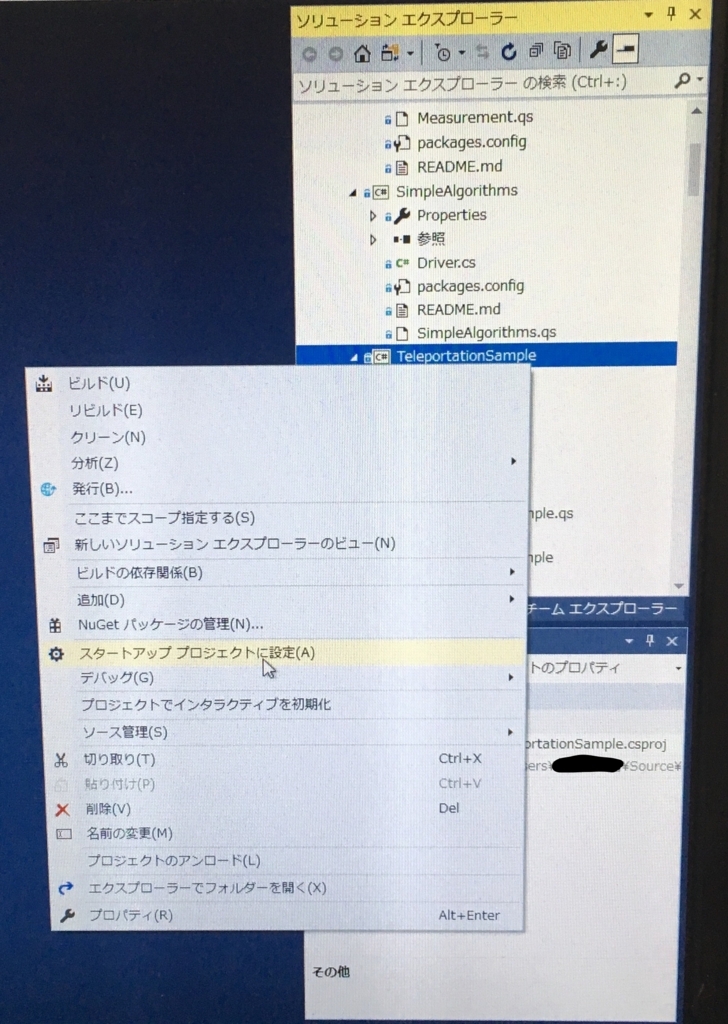
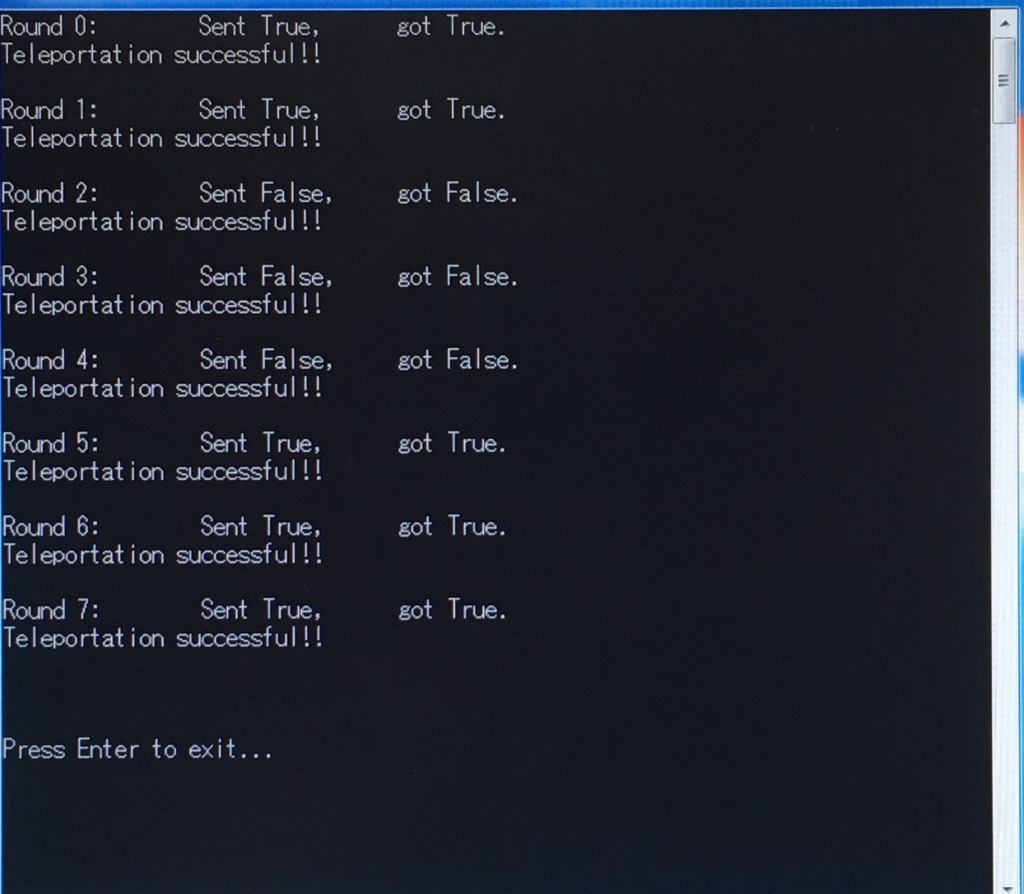
上の開始ボタンをクリックすると、Debug用プログラムが動きます。最終的にコマンドプロンプトが起動し、次のようなメッセージが表示されればおkです。表示されるTrue/Falseはランダムに変わるので、完全にこの通りでなくても大丈夫です。
量子コンピューターについて

現在使われている古典コンピューターでは、1ビット情報が「0」と「1」の2値で表現されています。物理的には電圧の高低で0と1を表現していることが多いです。
これに対して、量子コンピューターでは、1ビットとして「0」と「1」が確率的に重ね合わさった状態を用います(キュービット、Qubit)。しかし、この重ね合わせ状態をわれわれは直接観測によって捉えることができません。観測という行為によって重ね合わせ状態は破壊され、確率に応じて「0」か「1」に収束してしまうからです。
例えば、「0」が30%「1」が70%という確率で重ね合わさった状態を100個生成し、一つずつ観測していくと、0、1、1、0、1、0、1、1、1、0、1、1、... のように、観測値が得られます。100個分観測すれば、およそ30個が「0」、70個が「1」となります。
量子コンピューターでは、この確率的重ね合わせという特殊な性質を用いることで、離散フーリエ変換や素因数分解(RSA暗号の解読)を古典コンピューターより圧倒的に高速で解くことが出来るアルゴリズムが考案されており、量子コンピューターの性能がキャッチアップすれば、いずれ現実のものとなるでしょう。

今のところ、実在の量子コンピューターで古典コンピューターを超える性能を持つモノは存在しておらず、古典コンピューターを超える(=量子超越性)ことを目指した開発が進んでいます。
itpro.nikkeibp.co.jp
量子計算について
今後のために、量子計算における記号の定義や回路図の表現をまとめておきます。
量子計算において、1ビットの状態を表す2値(0と1)は$|0\rangle$や$|1\rangle$のように表記します。$| \rangle$は、ブラケット記法という量子力学特有の書き方です。
量子計算回路では、左から入力、右に進みながら、途中に設けられたゲートなどで操作を受けます。以下、具体的な入力・ゲート・出力を示しておきます。
Xゲートはキュービットを反転($|0\rangle \leftrightarrow |1\rangle$)させるゲートです。

Q#を書いてみよう
Qubitの操作・観測
まずは、Qubitの操作・観測を行ってみましょう。
メニューバーから、ファイル > 新規作成 > プロジェクトをクリックし、
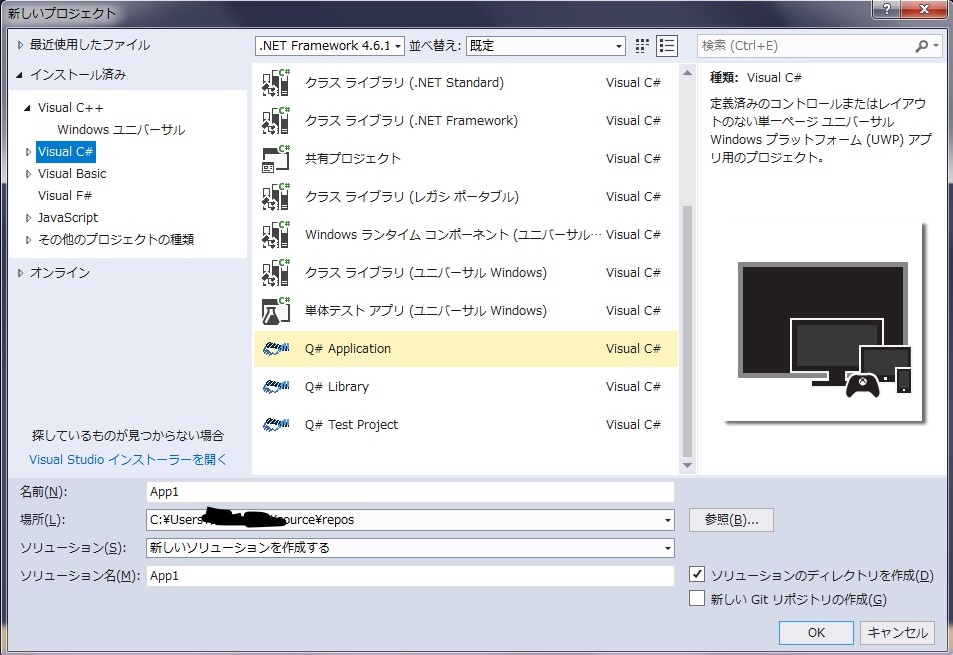
インストール済み > Visual C# > Q# Applicationを選択、名前を「Bell」としてOKボタンをクリックします。すると、次のようなコードが書かれたコーディング画面が表示されます。
namespace Quantum.Bell
{
open Microsoft.Quantum.Primitive;
operation Operation () : ()
{
body
{
}
}
}
ここで、ソリューション エクスプローラー内のOperation.qsを名前変更(右クリック)し、Bell.qsとします。
ここからコードを修正・加筆していきます。
operation Operation () : () を
operation Set (desired: Result, q1: Qubit) : ()に変更します。
さらに、body { } の内部に次のような処理を書き加えます。
namespace Quantum.Bell { open Microsoft.Quantum.Primitive; // "Set"関数を定義。Set関数は"q1"キュービットを"desired"の状態に変化させる operation Set (desired: Result, q1: Qubit) : () { body { let current = M(q1); // M(q1):q1キュービットの観測値を返す if (desired != current) { X(q1); // Xゲートによりq1キュービットをflipする } } } }
さらに、operation Set {}に続いて、次のoperation BellTest {}を追加します。
// "count"回数だけSet関数を実行する。引数"initial"はSet関数の引数"desired"として用いる // (Int,Int)は、返り値が2つ(int型とint型)であることを明示するためのもの operation BellTest (count : Int, initial: Result) : (Int,Int) { body { mutable numOnes = 0; using (qubits = Qubit[1]) { for (test in 1..count) // "1"から"count"までfor文ループ { Set (initial, qubits[0]); // Set関数により、"qubits[0]"は"initail"に変化 let res = M (qubits[0]); // "qubits[0]"を観測し、観測値を"res"に代入 // |1>が出現した回数を蓄積しておく if (res == One) { set numOnes = numOnes + 1; } } Set(Zero, qubits[0]); } return (count-numOnes, numOnes); // |0>、|1>の出現回数を返す } }
Q#の特徴として、letで不変変数を定義、mutableで可変変数を定義、setで算術結果などの代入、を行います。
次は、Driver.csファイルを編集します。.csファイルはC#で記述します。
using Microsoft.Quantum.Simulation.Core; using Microsoft.Quantum.Simulation.Simulators; namespace Quantum.Bell { class Driver { static void Main(string[] args) { } } }
main {}内に、次のコードを挿入します。
using (var sim = new QuantumSimulator()) { // Try initial values Result[] initials = new Result[] { Result.Zero, Result.One }; foreach (Result initial in initials) { // "BellTest"関数を実行し、結果を出力します。 var res = BellTest.Run(sim, 1000, initial).Result; var (numZeros, numOnes) = res; System.Console.WriteLine( $"Init:{initial,-4} 0s={numZeros,-4} 1s={numOnes,-4}"); } } System.Console.WriteLine("Press any key to continue..."); System.Console.ReadKey();
以上でQubit操作・観測のプログラムが完成しました。F5キー(または開始ボタン)を押して実行してください。次のような出力が表示されれば成功です!
Init:Zero 0s=1000 1s=0 Init:One 0s=0 1s=1000 Press any key to continue...
出力の解釈(1行目)としては、「初期状態として$|0\rangle$を用意し、これを観測した結果を蓄積する」というプロセスを1000回行った結果、$|0\rangle$が1000回得られ、$|1\rangle$が0回得られたという風になります。
また、"BellTest"関数内で、観測Mの前で、次のようにXゲートを作用すると、
X(qubits[0]);
let res = M (qubits[0]);このように反転(Flip)した結果が得られます。
Init:Zero 0s=0 1s=1000 Init:One 0s=1000 1s=0 Press any key to continue...
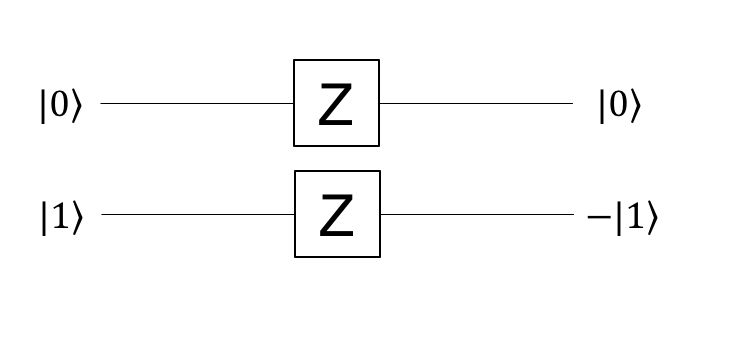
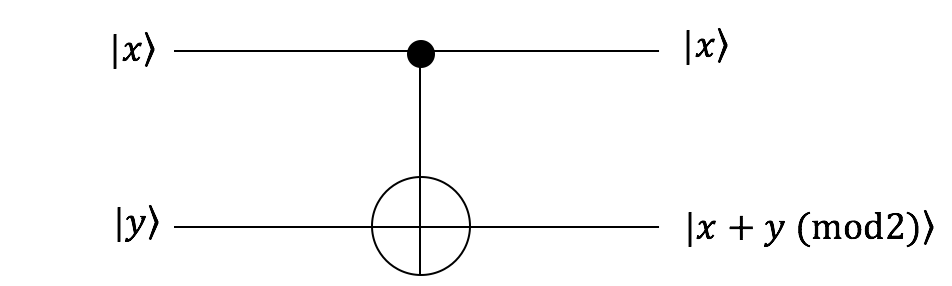
これは、量子計算の節で示した、次のような回路を動かしたことになります。

重ね合わせ
ここまでは、Qubitとは言っても、初期値が$|0\rangle$または$|1\rangle$、これをX(Xゲート)によるフリップ操作で$|1\rangle$または$|0\rangle$に変化させるというだけで、古典的な2値ビットと同じことしかやっていませんでした。
ここからは、完全な量子現象である、「重ね合わせ(superposition)」および「エンタングルメント(entanglement)」の状態を生成していきます。
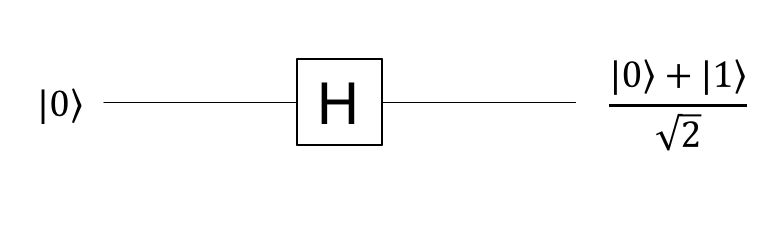
具体的には、次のようにキュービット状態を変化させる、アダマールゲート(Hadamard) Hを使います。
\begin{eqnarray}
\mid 0\rangle \to \frac{\mid 0\rangle + | 1\rangle}{\sqrt2} \\
\mid 1\rangle \to \frac{\mid 0\rangle - | 1\rangle}{\sqrt2}
\end{eqnarray}
重ね合わせ状態を観測した場合、観測値は状態に付いている係数の2乗に応じた確率で、その状態が得られます。
(具体例) $\frac{\mid 0\rangle + | 1\rangle}{\sqrt2}$のキュービットを観測すると、$\mid 0\rangle$に付いている係数は$\frac{1}{\sqrt 2}$、二乗して$\frac{1}{2}$、つまり50%の確率で$\mid 0\rangle$の観測値が得られます。$\mid 1\rangle$についても同様です。
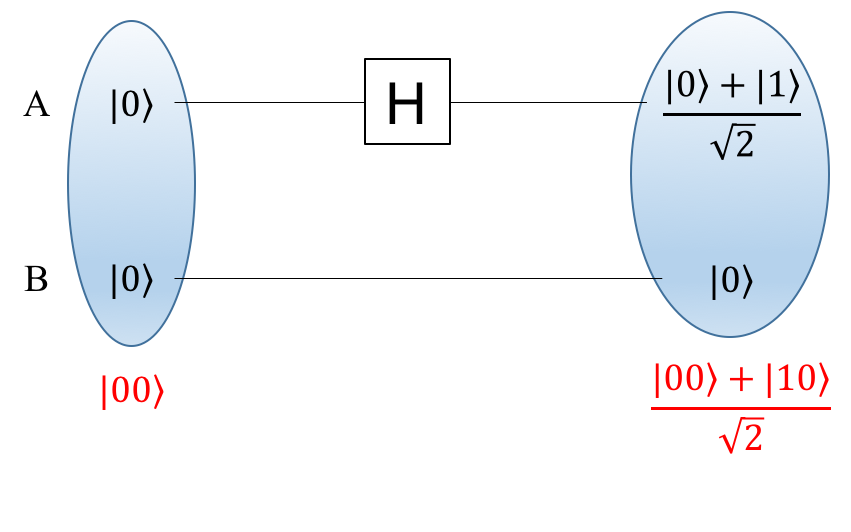
回路図は、次のようになります。

さて、実際にQ#で重ね合わせ状態を作成・観測してみましょう。
先のBell.qsにおいて、観測前に作用させたXゲートをHゲートに書き換えるだけです。
// X(qubits[0]); H(qubits[0]); let res = M (qubits[0]);
実行すると、
Init:Zero 0s=495 1s=505 Init:One 0s=492 1s=508 Press any key to continue...
このように$\mid 0\rangle$と$\mid 1\rangle$がおよそ半々の確率で観測されている、という結果になりました。
エンタングルメント
前節の「重ね合わせ」は1キュービット上における量子現象でした。ここからは、キュービットが2つ存在している場合について考えていきます。本格的に量子計算っぽい内容になっていきます。
2キュービットが存在する下のような回路を考えます。

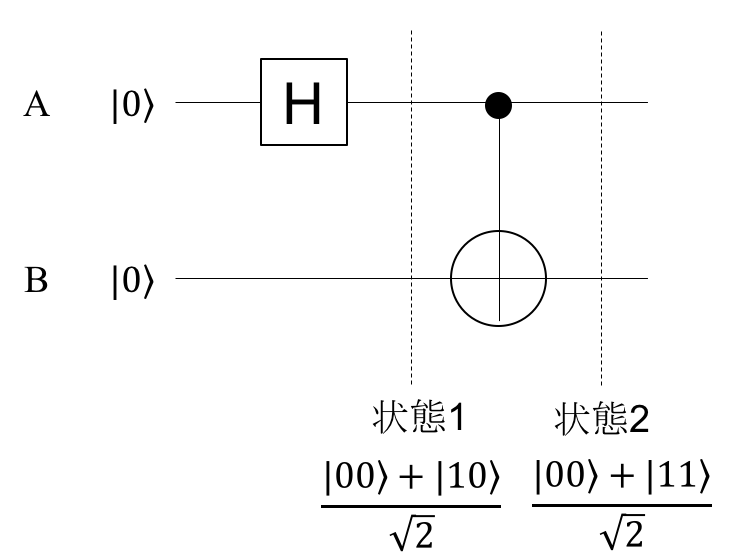
この状態2では、片方(A)を観測するともう一方(B)の状態が必然的に確定します。Aを観測して0ならばBが0、Aが1と出ればBも1になります。$\mid 01\rangle$や$\mid 10\rangle$といった状態が存在しないからです。(ちなみに状態1では、どちらか一方を観測しても他方に影響は及はず、このような2つのキュービット間の相関はありません。)
この、一方による観測で他方の状態が収束してしまうという物理現象は瞬時に伝わりますが、これを認めると直感的には信じられない事が起きます。例えば、エンタングル状態となった2つのキュービットの片方Aを地球に置いておき、片方Bを月へ持っていきます。Aを観測して$\mid 0\rangle$が得られた時、Bの状態は同時に$\mid 1\rangle$へと収束します。38万kmの距離を超えて瞬時に物理現象が伝わっているのです。
実際、これは量子力学の持つ欠陥(ありえない現象)として指摘され「EPRパラドックス」と呼ばれていました(1935年)。「EPR」は指摘を行った3人の研究者アインシュタイン、ポドルスキー、ローゼンの頭文字を取ったものです。現在では、この現象はパラドックスではなく実際に存在するもの(EPR相関)であると認識されており(「ベルの不等式」「アスペの実験」などによる、1980年代)、エンタングルメントを形成したキュービットを「 EPRペア」と呼ぶようになりました。
さて、ここからは実際にQ#を用いてEPRペアを作成してみましょう。
まずは、2キュービットの作成
using (qubits = Qubit[2])
loopごとの解放
Set(Zero, qubits[0]); Set(Zero, qubits[1]);
さらにSet関数による初期化、HゲートとCNOTゲートを設置します。
Set (initial, qubits[0]); Set (Zero, qubits[1]); H(qubits[0]); CNOT(qubits[0],qubits[1]); let res = M (qubits[0]);
まとめると、次のようになります。
operation BellTest (count : Int, initial: Result) : (Int,Int)
{
body
{
mutable numOnes = 0;
using (qubits = Qubit[2])
{
for (test in 1..count)
{
Set (initial, qubits[0]);
Set (Zero, qubits[1]);
H(qubits[0]);
CNOT(qubits[0],qubits[1]);
let res = M (qubits[0]);
// Count the number of ones we saw:
if (res == One)
{
set numOnes = numOnes + 1;
}
}
Set(Zero, qubits[0]);
Set(Zero, qubits[1]);
}
// Return number of times we saw a |0> and number of times we saw a |1>
return (count-numOnes, numOnes);
}
}
これでエンタングルメント状態が生成されます。
エンタングルメントしているかどうかを判定するために、2つの観測値が等しい場合をカウントします。
let res = M (qubits[0]); if (M (qubits[1]) == res) { set agree = agree + 1; } // Count the number of ones we saw: if (res == One) { set numOnes = numOnes + 1; }
これに合わせて、BellTest関数の返り値に関する部分を3変数に変更
operation BellTest (count : Int, initial: Result) : (Int,Int,Int)
return (count-numOnes, numOnes, agree);
さらに、Driver.csも3変数の受け取り、出力をするように変更します。
var (numZeros, numOnes, agree) = res;
System.Console.WriteLine(
$"Init:{initial,-4} 0s={numZeros,-4} 1s={numOnes,-4} agree={agree,-4}");
これを実行すると、
Init:Zero 0s=513 1s=487 agree=1000 Init:One 0s=510 1s=490 agree=1000
2つのキュービットが毎回同じ値を取る(独立でない)、つまりエンタングルしていることがわかります。
量子テレポーテーション
「量子テレポーテーション」とは、キュービットを(重ね合わせ状態を保ったまま)別の場所に送信する技術のことです。(物体を瞬間移動させたり、情報が超光速で伝わるといった現象を引き起こすものではありません。)
古典計算では、ビットのデータを読み込んで0か1を観測すれば、他の場所にそれと同じもの作る(コピーする)ことは容易です。しかし量子計算では、一度観測してしまえば重ね合わせ状態は消えてしまい、元の状態を復元することが出来なくなります。もちろん、得られるたった1つの観測値からどのような重ね合わせ状態であったのか知ることも出来ません。このような事情で、量子計算において量子状態を別の場所に移すには、キュービットを物理的に動かしてしまうか、エンタングルメントの性質を巧みに利用した量子テレポーテーションのアルゴリズムを用います。
問題設定としては、以下のようになります。AliceとBobの二人がいます。Aliceは何らかの係数で重ね合わさった状態 $\mid \psi \rangle = a\mid 0 \rangle + b\mid 1 \rangle$を所持しており、演算回路を通してBobに$\mid \psi \rangle$を送信したいと考えています。

答えとなる量子テレポーテーション回路図を示します。
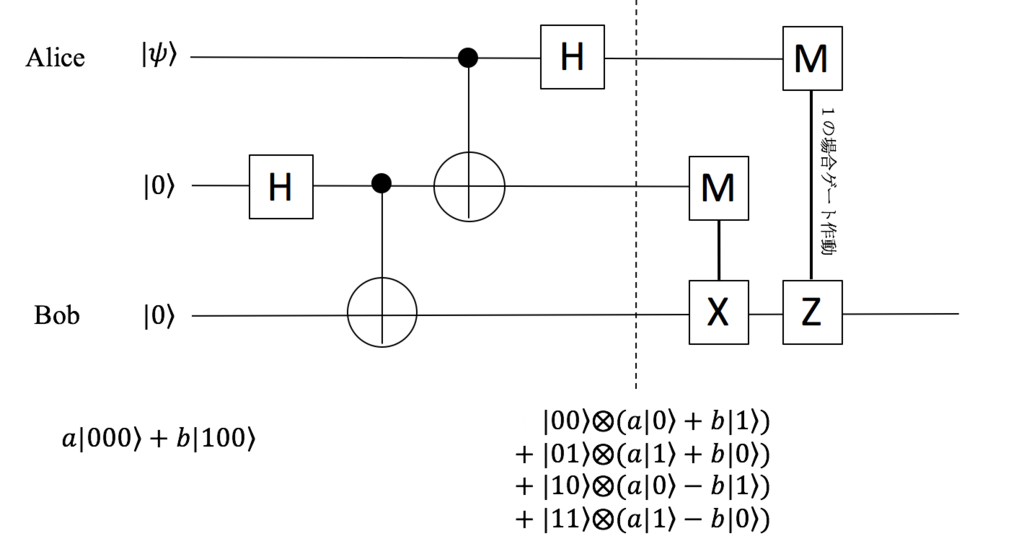
次のMゲートは観測を行うことを意味します。観測値が「1」の時、回路でつながったXゲートやZゲートが作動するとします。
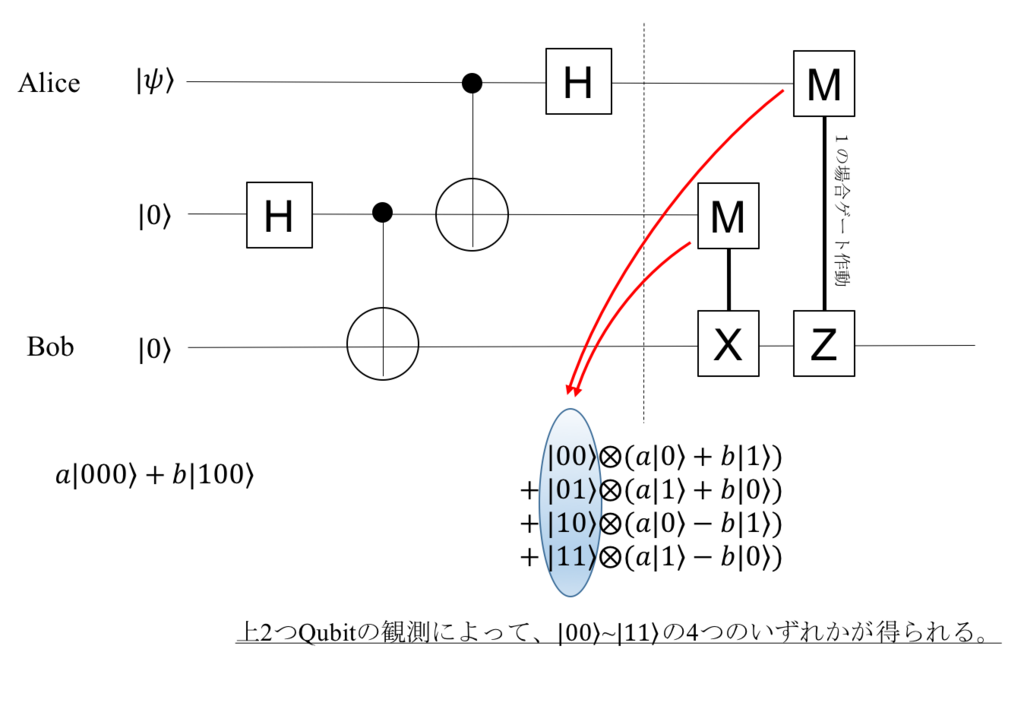

Aliceの持っていたキュービット情報の詳細(重ね合わせの係数a,bの具体値)自体は観測していませんが、たしかにBobの元へと同じ状態が送り届けられます。
Q#による実装を見てみましょう。コードは、以下のようになります。(参照:公式GitHub)
ここでは簡単のため、古典ビット("True"/"False"のメッセージを"1"/"0"と訳したもの)の転送を行っています。
Teleport関数において、上で示した量子計算が行われています。
namespace Microsoft.Quantum.Examples.Teleportation { open Microsoft.Quantum.Primitive; open Microsoft.Quantum.Canon; operation Teleport(msg : Qubit, there : Qubit) : () { body { using (register = Qubit[1]) { // "msg":Alice、"here":真ん中の入力、"there":Bobとなります let here = register[0]; H(here); CNOT(here, there); CNOT(msg, here); H(msg); if (M(msg) == One) { Z(there); } if (M(here) == One) { X(there); } Reset(here); } } } operation TeleportClassicalMessage(message : Bool) : Bool { body { mutable measurement = false; using (register = Qubit[2]) { // Ask for some qubits that we can use to teleport. let msg = register[0]; let there = register[1]; // Encode the message we want to send. if (message) { X(msg); } // Use the operation we defined above. Teleport(msg, there); // Check what message was sent. if (M(there) == One) { set measurement = true; } // Reset all of the qubits that we used before releasing // them. ResetAll(register); } return measurement; } } }
Driver.csは次のようになります。
using Microsoft.Quantum.Simulation.Simulators; using System.Linq; namespace Microsoft.Quantum.Examples.Teleportation { class Program { static void Main(string[] args) { var sim = new QuantumSimulator(); var rand = new System.Random(); foreach (var idxRun in Enumerable.Range(0, 8)) { var sent = rand.Next(2) == 0; var received = TeleportClassicalMessage.Run(sim, sent).Result; System.Console.WriteLine($"Round {idxRun}:\tSent {sent},\tgot {received}."); System.Console.WriteLine(sent == received ? "Teleportation successful!!\n" : "\n"); } System.Console.WriteLine("\n\nPress Enter to exit...\n\n"); System.Console.ReadLine(); } } }
次のように表示されれば、量子テレポーテーション成功です!
Round 0: Sent True, got True. Teleportation successful!! Round 1: Sent False, got False. Teleportation successful!! Round 2: Sent True, got True. Teleportation successful!! Round 3: Sent False, got False. Teleportation successful!! Round 4: Sent True, got True. Teleportation successful!! Round 5: Sent False, got False. Teleportation successful!! Round 6: Sent True, got True. Teleportation successful!! Round 7: Sent False, got False. Teleportation successful!! Press any key to exit...
参考サイトなど
・「Visual Studio 2017」、「Quantum Development Kit」のインストール
https://docs.microsoft.com/en-us/quantum/quantum-installconfig?view=qsharp-previewdocs.microsoft.com
・Bell状態の作成コード
docs.microsoft.com
・Microsoft量子コンピューターの写真を引用させて頂きました
With new Microsoft breakthroughs, general purpose quantum computing moves closer to reality | Stories
・量子コンピューターの勉強に使いました。とてもわかりやすかったです。

- 作者: 宮野健次郎,古澤明
- 出版社/メーカー: 日本評論社
- 発売日: 2016/03/03
- メディア: 単行本
- この商品を含むブログを見る