東大情報理工 創造情報 院試について (2018年度 冬院試)
この度、2018年2月に行われた東京大学大学院 情報理工学系研究科 創造情報学専攻の冬院試を受験し、合格しました。
自分の院試勉強内容、試験当日の事、冬院試問題(公式には公開されない)の再現pdf、その他感想などを載せておきます。
自分の経歴としては、学部は東大の材料系学科出身、修士は物理系学科に進学しましたが、いろいろ考えた結果、専攻分野を変更し情報系に行くことにしました(決めたのは2017年の11月頃)。冬院試をやっている専攻を見てる中でおもしろそうなテーマやってるラボを見つけて最終的に創造情報を受けることにした、という感じです。ここまでの経歴の通り、院試勉強開始時点でCS分野の知識はゼロからのスタートでした。
参考書
他の院試合格ブログで紹介されているやつを適当に見て良さげなやつに決めました。
結局まともに読んだのは次の4冊でした。
院試の流れ
12/1から勉強開始、ここから1ヶ月間で参考書4冊を一通りと、過去問3年分ぐらい解きました。
12/13に出願
2/7~2/9に本試験
2/20に郵送で結果が届きました。入学手続き用書類が同封されたデカイ封筒が速達で届きます。冬院試は掲示板発表無しの郵送のみなので、この合格発表までの1~2週間はずっとそわそわしてました。先輩方のTwitterとか遡って確認すると、去年は全く同じタイミング(試験終了の次々週の火曜日)、2年前は試験終了の次週の土曜に結果届いたみたいです。
受験当日
受験者は53人でした。合格者は例年5人とからしい(?)ので、倍率は10倍以上ということになります。周り見渡すと8割ぐらいは留学生でした。Twitterで検索すると、夏院試落ちた東大情報系の学生(ISer)も数人いたっぽいです。ただ留学生の学力レベルというのが未知過ぎてよくわかんないですね。この高倍率でも合格ラインがそこまで高くないっぽいことを考えると、あんまり点数取れてなさそうですが。
筆記試験
普通でした ここ2年ぐらいは問題の選択が出来なくなってます。必然的に語句問題という運ゲーをやらされます。
プログラミング試験
午前はコード書く。パソコン部屋に放置して昼休憩。午後は1人づつ部屋に呼ばれて、教員の見てる横で指示されたとおりに実行する。
面接
1人あたり5分ぐらい
控室で待機して、順番が来たら別室に呼ばれます。教員10人ぐらいの前で座って質問に答えるスタイル。
第一志望ラボの先生からの質問、「当該分野について何か勉強などしていますか?その内容について説明してください」。ラボで出た論文読んでますって言って、その内容を1分ぐらいで話しました。
進行役の教授からの質問、「卒論などこれまで行って来た研究についておしえて」
以上でした。配属希望は第二志望まで書いていたのですがそちらからは質問されずでした。
2018年度冬院試の問題再現
冬院試の問題は公式サイトでは公開されていません。試験終わった直後に一通り内容メモしていたので、それに基づいてLaTeXで書き起こしました。だいぶ適当なので参考程度に
筆記試験
プログラミング試験 (prog5.txt, prog6.txt, prog7.txt)
点数開示
点数開示申請を行ったので、結果出たら公開します。
体感としては筆記7割、プログラミング7割かなという感じでした。
→ 合格発表直後に院試点数開示申請して、1ヶ月後に結果が届きました。

平均点も合格最低点もわからず、自分の点数だけみても特になんとも言えないですね...
ただ、筆記プログラミング合わせて7割弱ということで、自分の体感値とそれほど大きなズレはありませんでした。
感想
筆記試験は、出題範囲が広い割に問題数が極端に少ない、ということで勉強量や実力が反映されにくい試験になってます。ただ最近は易化傾向で、何をさせたいのかわからないような問題も減って来ている気がします。
プログラミング試験は難化傾向にあると思います。過去問で一番むずかしいと思った2016年夏院試は、プログラミング3割でも受かっている人もいるらしいです。
studio-graph.hateblo.jp自分が出来ないやつは周りも出来てないんやろなあぐらいの気持ちでいきました。
いろいろ言ってきましたが、全体的に運ゲー要素が大きいということに尽きます。出題内容、受験者のレベル、合格者人数、合格基準などが不明瞭なまま、これからの生活を左右する高倍率試験を受けさせられるのはキツいです。ここ一本で受けるより情報学環とか併願してればよかったなと思いました。
参考サイトまとめ
・http://d.hatena.ne.jp/ma3tk/20110308/1299522668
(2011夏落ち冬合格)
頑張ったのは1月~
比率は英:数:専=120:120:240 ?
プログラミングは普通にやってれば半分くらい取れる
アルゴリズム関係、ハードウェア関係、機械関係(詳しく知らない)、語彙説明の4題で、1問も解けないようなことはない
計480点中の55%~60%がボーダーと言われている
・東京大学大学院 情報理工学系研究科に合格したようです - きたくち (他大出身)
(2015米大学院落ち冬合格)
応用情報を取ったのが5年くらい前、
冬入試で受かった人は4名程度
筆記ほぼ無勉、感覚的に5割程度、6割はまず取れてないだろうなーという出来
専門簡単すぎ Pyhtonでやった
1週間後くらいに結果が届いて、電話で配属先の研究室を確認するという流れ
得点開示したところ筆記・プログラミング共に6割強くらいでした。案外悪くなかったですね、謎採点だ。
・創造情報学専攻を受けた話 - ehlfin’s blog (学内出身、計数かな)
(2016夏は数理情報学落ち、2017冬合格)
夏の数理情報の点数開示
TOEFL(ITP) : 597/677 共通科目(数学):137/300 専門科目(数理情報学):132/300
冬
今年の冬入試の創造の受験者は45人、合格者は10人未満程度なのではないかと思う
TOEFL(iBT):89/120 共通科目(プログラミング):123/200 専門科目(創造情報学):210/300
プログラミング:標準入出力,ファイル操作,正規表現などをきちんとスムーズにこなせるように
実際の試験場では自分のPCとマニュアル1冊を持ち込める.ネットに繋がなければ何をしてもいいので,事前にpythonの標準入出力をまとめたQiitaと各種アルゴリズムのコードをまとめたサイトをwgetしておいた
口頭試問 「これを入力にして動かして」と言われるので入力して動かす.試験官はどうやら出力を見て正しいかどうか判定しているようだ 単に結果しか見ていないようだった
専門科目
出題範囲が異常に広い.これだけはやっておいたほうがいいと思われる分野を列挙しておく.
アルゴリズム、統計と機械学習の用語、論理回路、オペレーティングシステム、コンピュータアーキテクチャ、インターネット通信(TCP/IPとか)、コンピュータグラフィックスの用語
・東京大学大学院 情報理工学系研究科に合格して入学しました - タイトルって難しい。 (他大、半分情報系半分数理系の学科?)
(2014年8月と2015年2月に受験)
勉強期間は、夏入試も冬入試も10日〜14日くらい
某大学新聞に結果が載っていました。私の専攻は、64人(うち、15人内部生)受験、34人(うち、11人内部生)合格
Python3で解きました
学府→電情&CS→創造の順で解いていくと自然とできるようになるかと。
・創造情報学専攻(電子情報学専攻)の対策 - とんとんの院試ブログ (学内かな?)
(2014夏、電情の問題を選択で合格)
創造は知っていれば簡単だが、範囲が広くてどこから出るか分かりづらい
・電気・情報系院試の対策本まとめ、とくに東大情報理工創造情報 東北大情報科学 電通大ISむけ - ikegamのsuper seriousでsuper awesomeな勉強日記 (電気電子系出身)
大事な本はこれだけです。500ページくらいのもんでしょう。これならその木になれば二日くらいで一周できるはずです
”IT Text 離散数学”、”データ構造とアルゴリズム (新・情報 通信システム工学)”、”コンピュータアーキテクチャ (電子情報通信レクチャーシリーズ)”、”論理回路入門”ですべてです。
・情報理工学系研究科 創造情報学専攻の院試対策と参考書のまとめ : 東京大学大学院 院試対策と参考書まとめ (出身)
応用情報技術者試験合格程度の知識
定員:夏入試>>>>冬入試
語彙説明対策
アルゴリズム・システムアーキテクチャ>情報理論・離散数学>>プログラミング用語>暗号理論>人工知能・ロボット・CG>>データベース・ネットワーク
アルゴリズム→問1対策だけで良い
システムアーキテクチャ→問2の対策だけで良い
CG、ロボット→問3対策だけで良い
情報理論→Category:情報理論
統計学→Category:離散数学
プログラミング用語→プログラミング用語一覧 プログラミングパラダイム
暗号理論→暗号理論
人工知能→ Category:人工知能
データベース、ネットワーク→応用情報のテキストで勉強
勉強手順
wikiを見て軽く理解する→4~8行で説明出来るか確認する→出来たら次の言葉へ、出来なかったらwikiを読み直す
この繰り返しで語彙を増やすことができます。また、説明の際に図を書くと高い点数がもらえる傾向にあるそうなので、意識して勉強するといいかもしれません
新プログラミング言語「Q#」で量子テレポーテーション
Microsoftより前々から予告されていた、量子コンピューター向けの新プログラミング言語「Q#」及び開発キット「Quantum Development Kit」のプレビュー版が公開されました。
pc.watch.impress.co.jp
記事からの引用ですが、
(1)量子コンピューティング用のプログラミング言語「Q#」
(2)量子コンピューティングのシミュレーター(ローカルとAzure)
(3)量子コンピューティング向けコードのライブラリやサンプル
の3つが「Quantum Development Kit」には含まれています。
今回は、ローカル(Visual Studio)上において、Q#のコードを実装して量子計算のシミュレーションを行います。「準備編」および「Q#を書いてみよう」の内容は、公式HP(英語)に準拠して書いています(2017年12月15日時点)。
目次
準備編
Q#の開発環境を構築します。次の2つのソフトウェアのインストールが必要となります。
・「Visual Studio 2017」
・「Quantum Development Kit」 (今のところWindowsのみ対応)
「Visual Studio 2017」のインストール
こちらの公式サイトからダウンロードすることが出来ます。
www.visualstudio.com
Download for Windowsにカーソルを合わせ、Community 2017を選択するとダウンロード出来ます。
vs_community~から始まる名前の実行ファイルがダウンロードされているはずなので、これを実行しインストールします。インストールを進めていくと次の画面が表示されます。
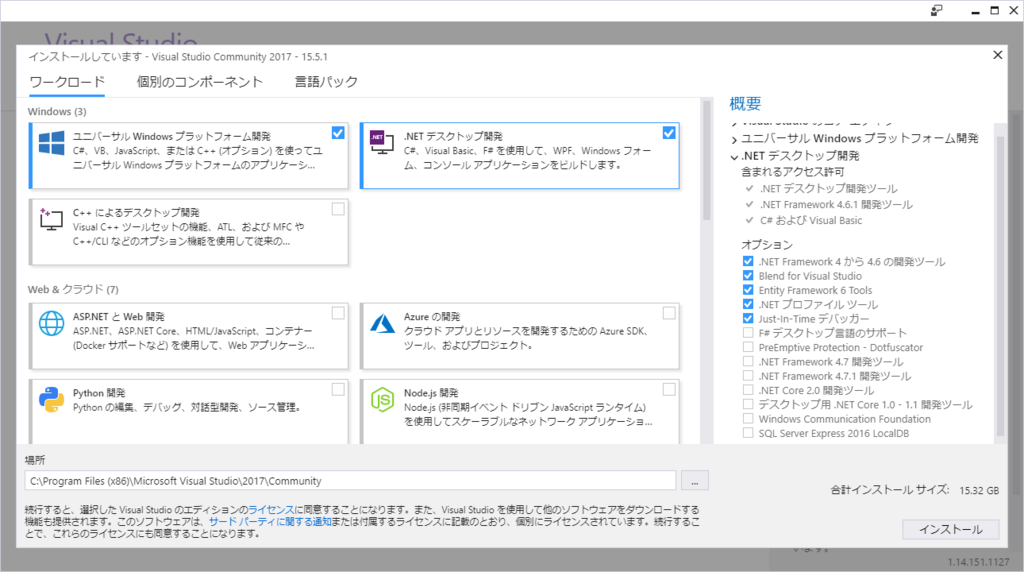
注意点として、「ユニバーサルWindowsプラットフォーム開発」と 「.NETデスクトップ開発」の2つの項目に必ずチェックを付けておきましょう。チェックを付けたら、右下のインストールをクリックします。インストールに成功すれば完了です。
「Quantum Development Kit」のインストール
こちらの公式HPに飛び、Download nowを選択。
次のページで名前や所属を入力し、Download nowボタンをクリックすると、次のページが表示されます。
ここでDownloadをクリックします。
QsharpVSIX.vsixというファイルがダウンロードされているはずなので、実行します。
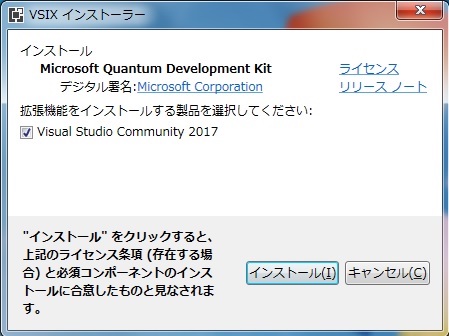
Visual Studioが正しくインストールされていれば、.vsixがVisual Studioの拡張インストールパッケージであることが認識され、次のようなインストール画面が表示さあれます。
動作確認
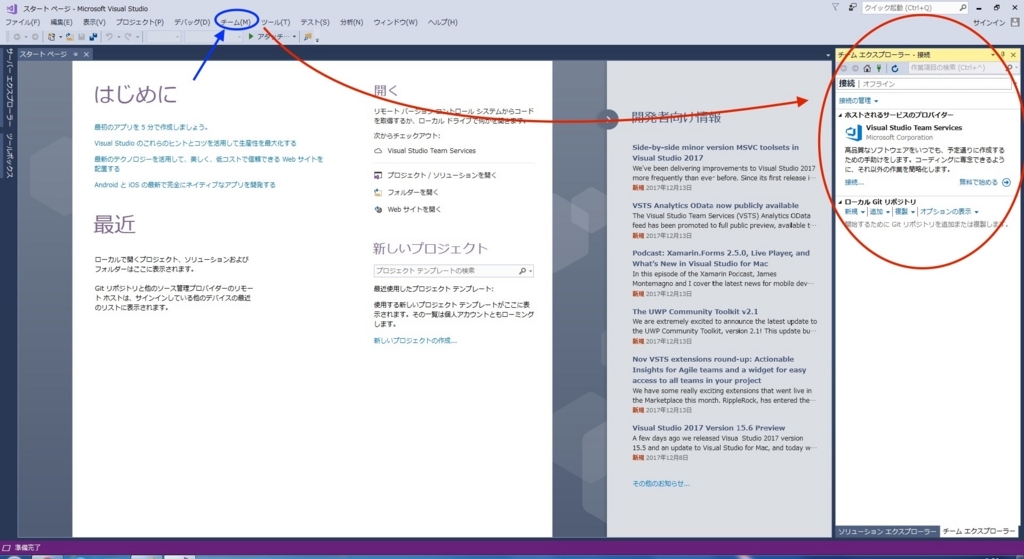
Visual Studioを起動し、メニューバーのチーム>接続の管理をクリックします。画面右にチーム エクスプローラーが出現します。
ローカルGitリポジトリの下の複製をクリックします。
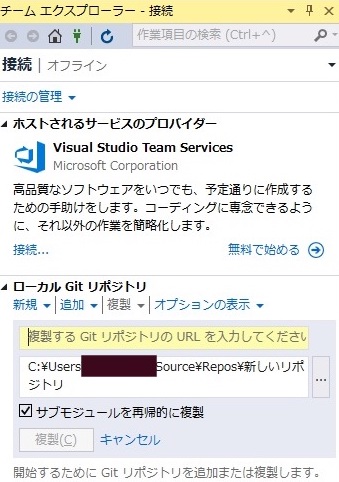
https://github.com/Microsoft/Quantum.gitと入力し、複製をクリックします。複製が終わると、チーム エクスプローラーがソリューションエクスプローラーに切り替わります。
切り替わったソリューションエクスプローラー内にある、QsharpLIbraries.slnをダブルクリックします。
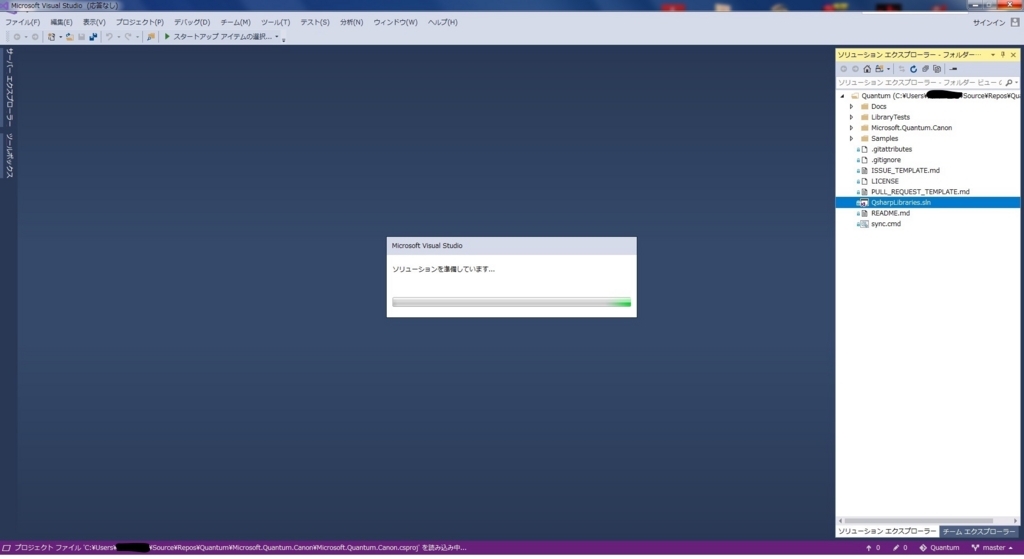
何らかのインストールが要求される場合があるので、指示に従ってインストールを行います。
次に、ソリューションエクスプローラー内のSamples > 0.Introduction > TeleportationSampleを右クリック、スタートアッププロジェクトに設定を左クリックします。
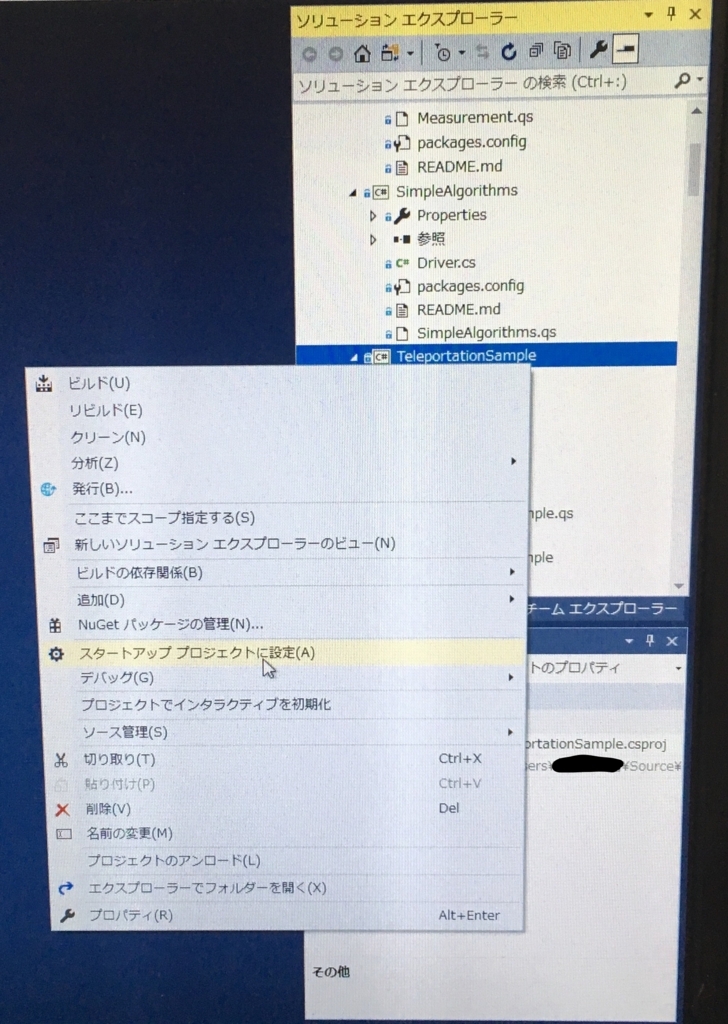
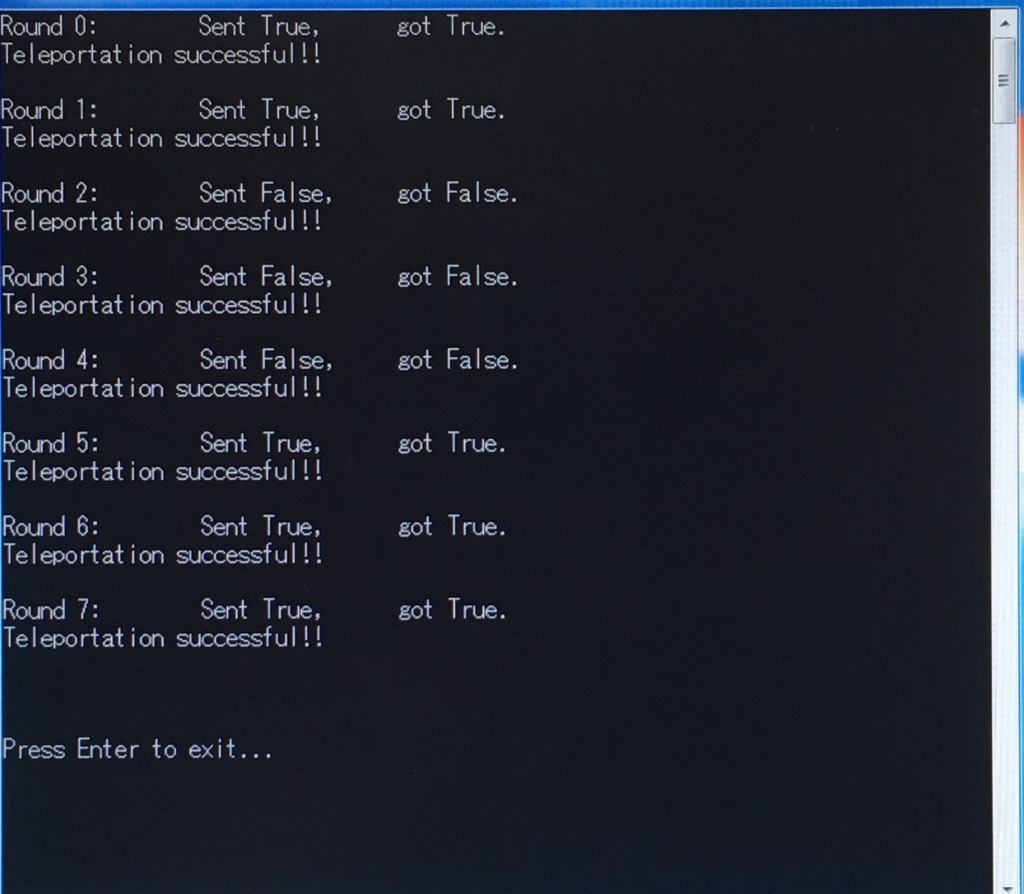
上の開始ボタンをクリックすると、Debug用プログラムが動きます。最終的にコマンドプロンプトが起動し、次のようなメッセージが表示されればおkです。表示されるTrue/Falseはランダムに変わるので、完全にこの通りでなくても大丈夫です。
量子コンピューターについて

現在使われている古典コンピューターでは、1ビット情報が「0」と「1」の2値で表現されています。物理的には電圧の高低で0と1を表現していることが多いです。
これに対して、量子コンピューターでは、1ビットとして「0」と「1」が確率的に重ね合わさった状態を用います(キュービット、Qubit)。しかし、この重ね合わせ状態をわれわれは直接観測によって捉えることができません。観測という行為によって重ね合わせ状態は破壊され、確率に応じて「0」か「1」に収束してしまうからです。
例えば、「0」が30%「1」が70%という確率で重ね合わさった状態を100個生成し、一つずつ観測していくと、0、1、1、0、1、0、1、1、1、0、1、1、... のように、観測値が得られます。100個分観測すれば、およそ30個が「0」、70個が「1」となります。
量子コンピューターでは、この確率的重ね合わせという特殊な性質を用いることで、離散フーリエ変換や素因数分解(RSA暗号の解読)を古典コンピューターより圧倒的に高速で解くことが出来るアルゴリズムが考案されており、量子コンピューターの性能がキャッチアップすれば、いずれ現実のものとなるでしょう。

今のところ、実在の量子コンピューターで古典コンピューターを超える性能を持つモノは存在しておらず、古典コンピューターを超える(=量子超越性)ことを目指した開発が進んでいます。
itpro.nikkeibp.co.jp
量子計算について
今後のために、量子計算における記号の定義や回路図の表現をまとめておきます。
量子計算において、1ビットの状態を表す2値(0と1)は$|0\rangle$や$|1\rangle$のように表記します。$| \rangle$は、ブラケット記法という量子力学特有の書き方です。
量子計算回路では、左から入力、右に進みながら、途中に設けられたゲートなどで操作を受けます。以下、具体的な入力・ゲート・出力を示しておきます。
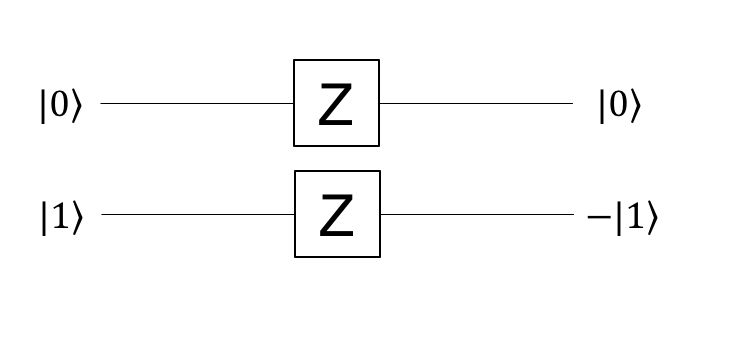
Xゲートはキュービットを反転($|0\rangle \leftrightarrow |1\rangle$)させるゲートです。

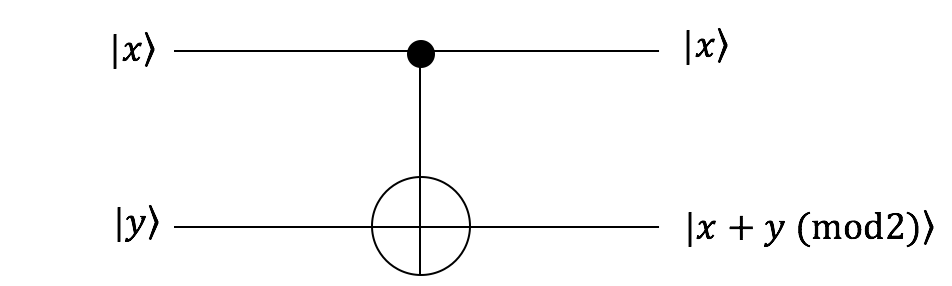
Q#を書いてみよう
Qubitの操作・観測
まずは、Qubitの操作・観測を行ってみましょう。
メニューバーから、ファイル > 新規作成 > プロジェクトをクリックし、
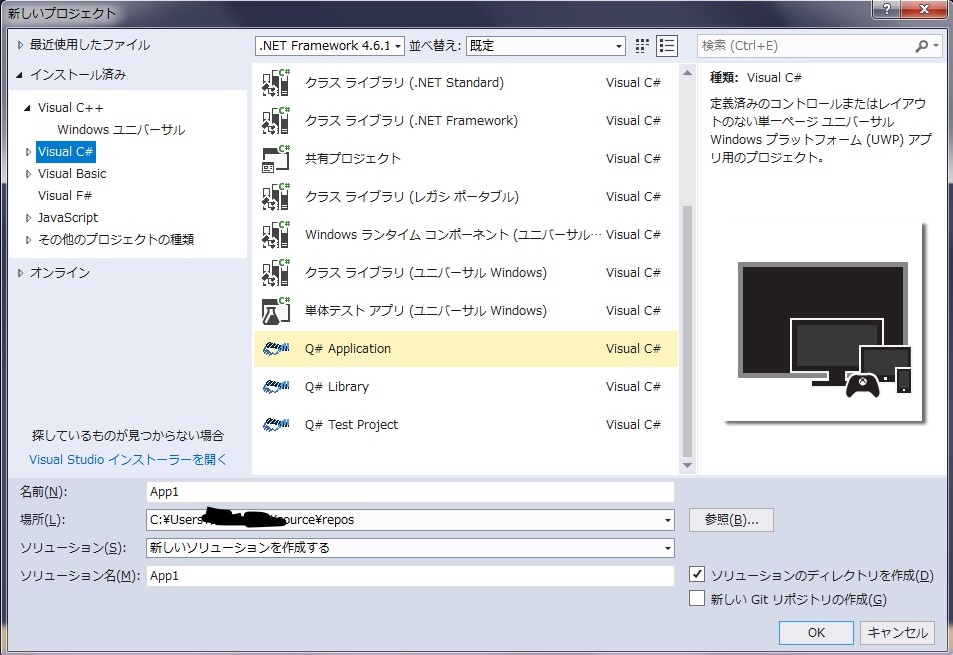
インストール済み > Visual C# > Q# Applicationを選択、名前を「Bell」としてOKボタンをクリックします。すると、次のようなコードが書かれたコーディング画面が表示されます。
namespace Quantum.Bell
{
open Microsoft.Quantum.Primitive;
operation Operation () : ()
{
body
{
}
}
}
ここで、ソリューション エクスプローラー内のOperation.qsを名前変更(右クリック)し、Bell.qsとします。
ここからコードを修正・加筆していきます。
operation Operation () : () を
operation Set (desired: Result, q1: Qubit) : ()に変更します。
さらに、body { } の内部に次のような処理を書き加えます。
namespace Quantum.Bell { open Microsoft.Quantum.Primitive; // "Set"関数を定義。Set関数は"q1"キュービットを"desired"の状態に変化させる operation Set (desired: Result, q1: Qubit) : () { body { let current = M(q1); // M(q1):q1キュービットの観測値を返す if (desired != current) { X(q1); // Xゲートによりq1キュービットをflipする } } } }
さらに、operation Set {}に続いて、次のoperation BellTest {}を追加します。
// "count"回数だけSet関数を実行する。引数"initial"はSet関数の引数"desired"として用いる // (Int,Int)は、返り値が2つ(int型とint型)であることを明示するためのもの operation BellTest (count : Int, initial: Result) : (Int,Int) { body { mutable numOnes = 0; using (qubits = Qubit[1]) { for (test in 1..count) // "1"から"count"までfor文ループ { Set (initial, qubits[0]); // Set関数により、"qubits[0]"は"initail"に変化 let res = M (qubits[0]); // "qubits[0]"を観測し、観測値を"res"に代入 // |1>が出現した回数を蓄積しておく if (res == One) { set numOnes = numOnes + 1; } } Set(Zero, qubits[0]); } return (count-numOnes, numOnes); // |0>、|1>の出現回数を返す } }
Q#の特徴として、letで不変変数を定義、mutableで可変変数を定義、setで算術結果などの代入、を行います。
次は、Driver.csファイルを編集します。.csファイルはC#で記述します。
using Microsoft.Quantum.Simulation.Core; using Microsoft.Quantum.Simulation.Simulators; namespace Quantum.Bell { class Driver { static void Main(string[] args) { } } }
main {}内に、次のコードを挿入します。
using (var sim = new QuantumSimulator()) { // Try initial values Result[] initials = new Result[] { Result.Zero, Result.One }; foreach (Result initial in initials) { // "BellTest"関数を実行し、結果を出力します。 var res = BellTest.Run(sim, 1000, initial).Result; var (numZeros, numOnes) = res; System.Console.WriteLine( $"Init:{initial,-4} 0s={numZeros,-4} 1s={numOnes,-4}"); } } System.Console.WriteLine("Press any key to continue..."); System.Console.ReadKey();
以上でQubit操作・観測のプログラムが完成しました。F5キー(または開始ボタン)を押して実行してください。次のような出力が表示されれば成功です!
Init:Zero 0s=1000 1s=0 Init:One 0s=0 1s=1000 Press any key to continue...
出力の解釈(1行目)としては、「初期状態として$|0\rangle$を用意し、これを観測した結果を蓄積する」というプロセスを1000回行った結果、$|0\rangle$が1000回得られ、$|1\rangle$が0回得られたという風になります。
また、"BellTest"関数内で、観測Mの前で、次のようにXゲートを作用すると、
X(qubits[0]);
let res = M (qubits[0]);このように反転(Flip)した結果が得られます。
Init:Zero 0s=0 1s=1000 Init:One 0s=1000 1s=0 Press any key to continue...
これは、量子計算の節で示した、次のような回路を動かしたことになります。

重ね合わせ
ここまでは、Qubitとは言っても、初期値が$|0\rangle$または$|1\rangle$、これをX(Xゲート)によるフリップ操作で$|1\rangle$または$|0\rangle$に変化させるというだけで、古典的な2値ビットと同じことしかやっていませんでした。
ここからは、完全な量子現象である、「重ね合わせ(superposition)」および「エンタングルメント(entanglement)」の状態を生成していきます。
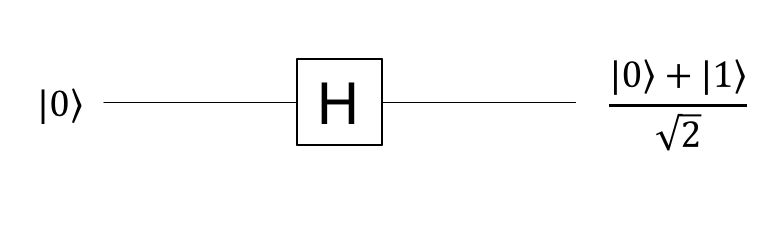
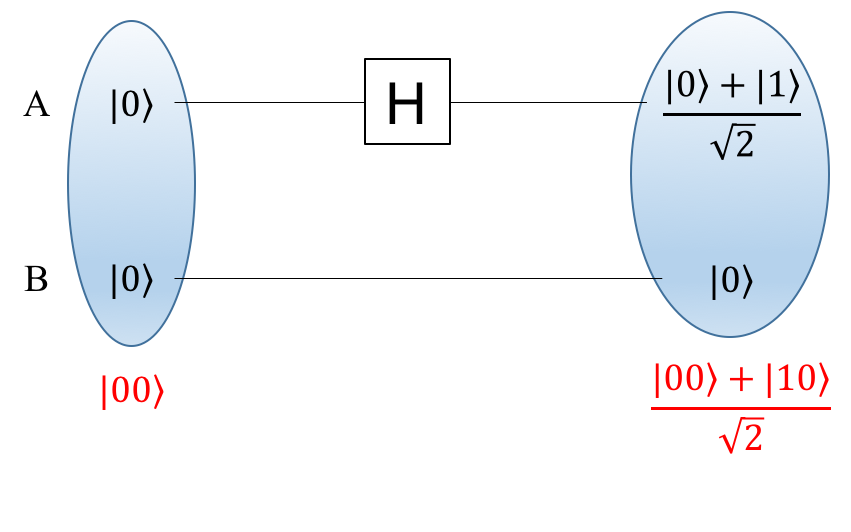
具体的には、次のようにキュービット状態を変化させる、アダマールゲート(Hadamard) Hを使います。
\begin{eqnarray}
\mid 0\rangle \to \frac{\mid 0\rangle + | 1\rangle}{\sqrt2} \\
\mid 1\rangle \to \frac{\mid 0\rangle - | 1\rangle}{\sqrt2}
\end{eqnarray}
重ね合わせ状態を観測した場合、観測値は状態に付いている係数の2乗に応じた確率で、その状態が得られます。
(具体例) $\frac{\mid 0\rangle + | 1\rangle}{\sqrt2}$のキュービットを観測すると、$\mid 0\rangle$に付いている係数は$\frac{1}{\sqrt 2}$、二乗して$\frac{1}{2}$、つまり50%の確率で$\mid 0\rangle$の観測値が得られます。$\mid 1\rangle$についても同様です。
回路図は、次のようになります。

さて、実際にQ#で重ね合わせ状態を作成・観測してみましょう。
先のBell.qsにおいて、観測前に作用させたXゲートをHゲートに書き換えるだけです。
// X(qubits[0]); H(qubits[0]); let res = M (qubits[0]);
実行すると、
Init:Zero 0s=495 1s=505 Init:One 0s=492 1s=508 Press any key to continue...
このように$\mid 0\rangle$と$\mid 1\rangle$がおよそ半々の確率で観測されている、という結果になりました。
エンタングルメント
前節の「重ね合わせ」は1キュービット上における量子現象でした。ここからは、キュービットが2つ存在している場合について考えていきます。本格的に量子計算っぽい内容になっていきます。
2キュービットが存在する下のような回路を考えます。

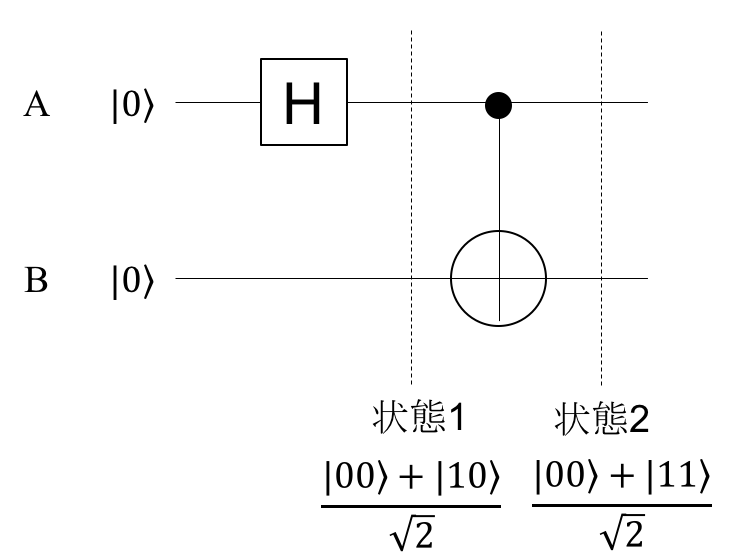
この状態2では、片方(A)を観測するともう一方(B)の状態が必然的に確定します。Aを観測して0ならばBが0、Aが1と出ればBも1になります。$\mid 01\rangle$や$\mid 10\rangle$といった状態が存在しないからです。(ちなみに状態1では、どちらか一方を観測しても他方に影響は及はず、このような2つのキュービット間の相関はありません。)
この、一方による観測で他方の状態が収束してしまうという物理現象は瞬時に伝わりますが、これを認めると直感的には信じられない事が起きます。例えば、エンタングル状態となった2つのキュービットの片方Aを地球に置いておき、片方Bを月へ持っていきます。Aを観測して$\mid 0\rangle$が得られた時、Bの状態は同時に$\mid 1\rangle$へと収束します。38万kmの距離を超えて瞬時に物理現象が伝わっているのです。
実際、これは量子力学の持つ欠陥(ありえない現象)として指摘され「EPRパラドックス」と呼ばれていました(1935年)。「EPR」は指摘を行った3人の研究者アインシュタイン、ポドルスキー、ローゼンの頭文字を取ったものです。現在では、この現象はパラドックスではなく実際に存在するもの(EPR相関)であると認識されており(「ベルの不等式」「アスペの実験」などによる、1980年代)、エンタングルメントを形成したキュービットを「 EPRペア」と呼ぶようになりました。
さて、ここからは実際にQ#を用いてEPRペアを作成してみましょう。
まずは、2キュービットの作成
using (qubits = Qubit[2])
loopごとの解放
Set(Zero, qubits[0]); Set(Zero, qubits[1]);
さらにSet関数による初期化、HゲートとCNOTゲートを設置します。
Set (initial, qubits[0]); Set (Zero, qubits[1]); H(qubits[0]); CNOT(qubits[0],qubits[1]); let res = M (qubits[0]);
まとめると、次のようになります。
operation BellTest (count : Int, initial: Result) : (Int,Int)
{
body
{
mutable numOnes = 0;
using (qubits = Qubit[2])
{
for (test in 1..count)
{
Set (initial, qubits[0]);
Set (Zero, qubits[1]);
H(qubits[0]);
CNOT(qubits[0],qubits[1]);
let res = M (qubits[0]);
// Count the number of ones we saw:
if (res == One)
{
set numOnes = numOnes + 1;
}
}
Set(Zero, qubits[0]);
Set(Zero, qubits[1]);
}
// Return number of times we saw a |0> and number of times we saw a |1>
return (count-numOnes, numOnes);
}
}
これでエンタングルメント状態が生成されます。
エンタングルメントしているかどうかを判定するために、2つの観測値が等しい場合をカウントします。
let res = M (qubits[0]); if (M (qubits[1]) == res) { set agree = agree + 1; } // Count the number of ones we saw: if (res == One) { set numOnes = numOnes + 1; }
これに合わせて、BellTest関数の返り値に関する部分を3変数に変更
operation BellTest (count : Int, initial: Result) : (Int,Int,Int)
return (count-numOnes, numOnes, agree);
さらに、Driver.csも3変数の受け取り、出力をするように変更します。
var (numZeros, numOnes, agree) = res;
System.Console.WriteLine(
$"Init:{initial,-4} 0s={numZeros,-4} 1s={numOnes,-4} agree={agree,-4}");
これを実行すると、
Init:Zero 0s=513 1s=487 agree=1000 Init:One 0s=510 1s=490 agree=1000
2つのキュービットが毎回同じ値を取る(独立でない)、つまりエンタングルしていることがわかります。
量子テレポーテーション
「量子テレポーテーション」とは、キュービットを(重ね合わせ状態を保ったまま)別の場所に送信する技術のことです。(物体を瞬間移動させたり、情報が超光速で伝わるといった現象を引き起こすものではありません。)
古典計算では、ビットのデータを読み込んで0か1を観測すれば、他の場所にそれと同じもの作る(コピーする)ことは容易です。しかし量子計算では、一度観測してしまえば重ね合わせ状態は消えてしまい、元の状態を復元することが出来なくなります。もちろん、得られるたった1つの観測値からどのような重ね合わせ状態であったのか知ることも出来ません。このような事情で、量子計算において量子状態を別の場所に移すには、キュービットを物理的に動かしてしまうか、エンタングルメントの性質を巧みに利用した量子テレポーテーションのアルゴリズムを用います。
問題設定としては、以下のようになります。AliceとBobの二人がいます。Aliceは何らかの係数で重ね合わさった状態 $\mid \psi \rangle = a\mid 0 \rangle + b\mid 1 \rangle$を所持しており、演算回路を通してBobに$\mid \psi \rangle$を送信したいと考えています。

答えとなる量子テレポーテーション回路図を示します。
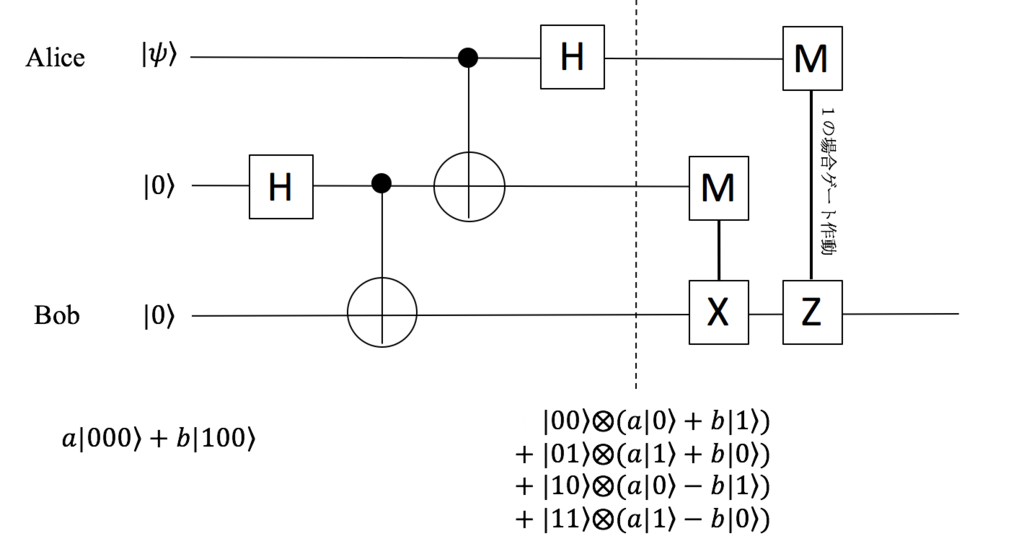
次のMゲートは観測を行うことを意味します。観測値が「1」の時、回路でつながったXゲートやZゲートが作動するとします。
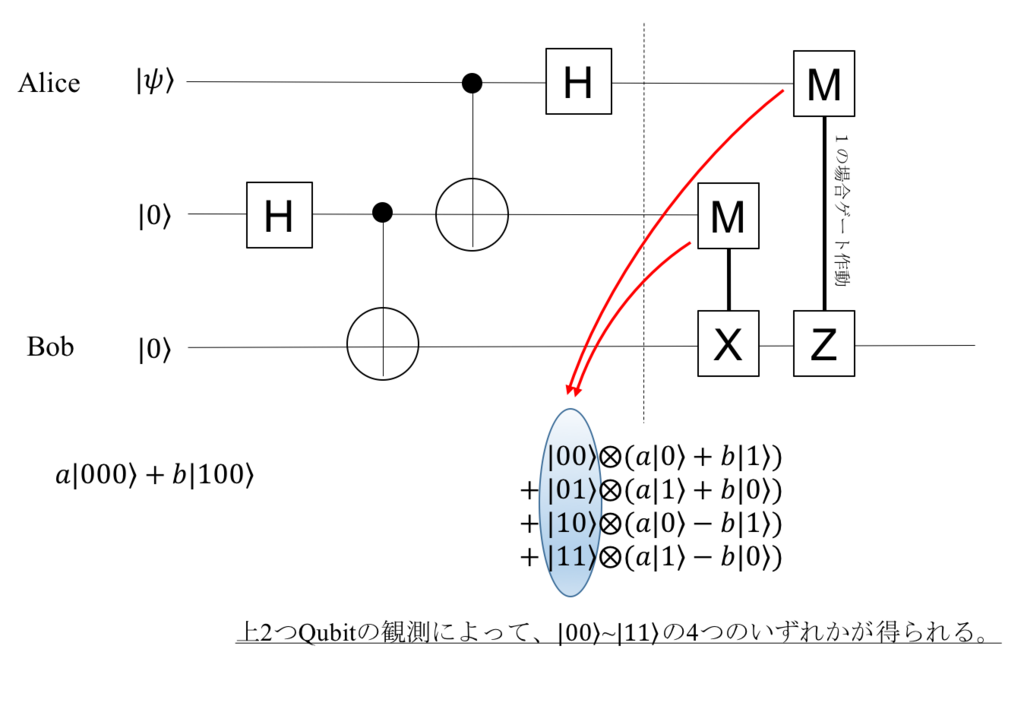

Aliceの持っていたキュービット情報の詳細(重ね合わせの係数a,bの具体値)自体は観測していませんが、たしかにBobの元へと同じ状態が送り届けられます。
Q#による実装を見てみましょう。コードは、以下のようになります。(参照:公式GitHub)
ここでは簡単のため、古典ビット("True"/"False"のメッセージを"1"/"0"と訳したもの)の転送を行っています。
Teleport関数において、上で示した量子計算が行われています。
namespace Microsoft.Quantum.Examples.Teleportation { open Microsoft.Quantum.Primitive; open Microsoft.Quantum.Canon; operation Teleport(msg : Qubit, there : Qubit) : () { body { using (register = Qubit[1]) { // "msg":Alice、"here":真ん中の入力、"there":Bobとなります let here = register[0]; H(here); CNOT(here, there); CNOT(msg, here); H(msg); if (M(msg) == One) { Z(there); } if (M(here) == One) { X(there); } Reset(here); } } } operation TeleportClassicalMessage(message : Bool) : Bool { body { mutable measurement = false; using (register = Qubit[2]) { // Ask for some qubits that we can use to teleport. let msg = register[0]; let there = register[1]; // Encode the message we want to send. if (message) { X(msg); } // Use the operation we defined above. Teleport(msg, there); // Check what message was sent. if (M(there) == One) { set measurement = true; } // Reset all of the qubits that we used before releasing // them. ResetAll(register); } return measurement; } } }
Driver.csは次のようになります。
using Microsoft.Quantum.Simulation.Simulators; using System.Linq; namespace Microsoft.Quantum.Examples.Teleportation { class Program { static void Main(string[] args) { var sim = new QuantumSimulator(); var rand = new System.Random(); foreach (var idxRun in Enumerable.Range(0, 8)) { var sent = rand.Next(2) == 0; var received = TeleportClassicalMessage.Run(sim, sent).Result; System.Console.WriteLine($"Round {idxRun}:\tSent {sent},\tgot {received}."); System.Console.WriteLine(sent == received ? "Teleportation successful!!\n" : "\n"); } System.Console.WriteLine("\n\nPress Enter to exit...\n\n"); System.Console.ReadLine(); } } }
次のように表示されれば、量子テレポーテーション成功です!
Round 0: Sent True, got True. Teleportation successful!! Round 1: Sent False, got False. Teleportation successful!! Round 2: Sent True, got True. Teleportation successful!! Round 3: Sent False, got False. Teleportation successful!! Round 4: Sent True, got True. Teleportation successful!! Round 5: Sent False, got False. Teleportation successful!! Round 6: Sent True, got True. Teleportation successful!! Round 7: Sent False, got False. Teleportation successful!! Press any key to exit...
参考サイトなど
・「Visual Studio 2017」、「Quantum Development Kit」のインストール
https://docs.microsoft.com/en-us/quantum/quantum-installconfig?view=qsharp-previewdocs.microsoft.com
・Bell状態の作成コード
docs.microsoft.com
・Microsoft量子コンピューターの写真を引用させて頂きました
With new Microsoft breakthroughs, general purpose quantum computing moves closer to reality | Stories
・量子コンピューターの勉強に使いました。とてもわかりやすかったです。

- 作者: 宮野健次郎,古澤明
- 出版社/メーカー: 日本評論社
- 発売日: 2016/03/03
- メディア: 単行本
- この商品を含むブログを見る
海洋科学野外実習
11月8日~11月10日に東京大学大学院・生物科学専攻で開講の海洋科学野外実習に参加してきました。


目次
1日目
11/8(水) 7時前起き、出家。JR久里浜駅に向かう。神奈川の南端のほう。

ちょうどお仕事でやっていたDQNでブロック崩しAI(土曜締め切り)が完成しておらず、電車の中でデバッグ作業。駅着いたら既に全員集合してた。8人しかいない。最大20人とかだったので予想より少ない。

タクシーでフェリー乗り場へ。フェリーは日常的に運行しているのに乗せてもらった。久里浜(神奈川)-金谷(千葉)を結ぶ路線。車を久里浜に置いて、フェリーで千葉のゴルフ場へ行くゴルフ客がメインらしい。

10時頃にフェリー乗船。一般客なら立ち入り禁止区域となっている、船の後ろ端で東京湾のXBT(水温)測定。一個5000円する測定器を使い捨てで海にどんどん投げ込む。ガチ研究で使う高性能なやつやと数万円のものを使うらしい。やば



金谷についたら次の出港まで船内を見学。一般人は絶対に入れない場所。貴重な写真(?)







帰りも水温測定。終わった後は港で昼飯。横須賀名物海軍カレー

この後、タクシーで近くの港湾空港技術研究所へ向かう。ペリー来校の地らしく、途中ペリー記念公園とかの横を通る。

港湾空港技術研究所を見学。たまたま同じ時間に申し込んでいた、海上自衛隊の人たちと一緒に回る。金属材料の海際での劣化観察実験、臨界生物の飼育・観察所など。


最後に有名な超大型の人工津波発生器の見学もしました。
バスと電車で三崎臨界実験場へ。横浜のJKスカートが(ry

夕飯の後は東京湾の水温測定結果の解析。解析データから、東京湾を横断するルートでの断面、深さ方向の水温分布がわかった。水温分布は久里浜側で低温層が上に、高温層が下という物理的にはおかしな現象が起きている。これは南から流れこむ温かい黒潮vs東京湾に来たから流れ込む冷たい川の水がぶつかっている。コリオリ力で黒潮と川水の流れは進行方向右にズレる。金谷側では黒潮が優勢となり、逆転温度分布は中和される。(水温分布の画像撮り忘れてしまった)


宿泊棟に鎮座する初代iMac


3日目
マグロのせり市場見学。

神奈川県水産技術センター見学。センター長はさかなクンの古い知り合いらしい。


午後、臨界丸に乗船してROVを行う。水中版ドローン。三日間の疲れからか、乗船中ほぼ爆睡していた



正準相関分析と固有値問題
正準相関分析がいかにして固有値問題へと帰着されるのかについて。
(PDFverはこちら)
目次
正準相関分析とは
一次元データ同士の相関は、次の図にあるように散布図としてプロットした場合にどれだけ一直線に並んでいるか、という「相関係数」の指標で評価出来ます。これは直感的にわかりやすく、数値計算も2データについての共分散と分散の値から簡単に計算出来ます。
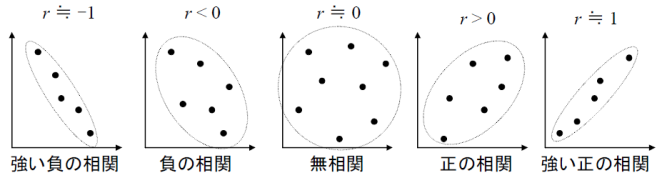
しかし、現実には2次元以上の多次元データが与えられる場合ももちろんあります。

さて、2次元以上の多次元データ同士がどれほど相関を持つか、をどのように判断すればよいでしょうか。ここで「正準相関分析」という手法が登場します。正準相関分析では多次元データを1次元に変換し、変換後の1次元データ同士について相関係数を求めます。この際、相関係数が最も大きくなるような変換方法を選ぶものとします。先日記事を書いた「主成分分析」においては、データの次元の削減を行い、その際削減後の分散が最大となる変換を選びました。正準相関分析もこれと非常に似ていると言えます。さらに共通する重大な特徴として、正準相関分析と主成分分析はともに固有値問題へと帰着されるということが挙げられます。以下では、具体的に正準相関分析の手法を詳しく見ていきます。
blog.aidemy.net
多次元データ
多次元データがN個あるとする。$\vec{X}^{(1)}、\vec{X}^{(2)} \cdot \cdot \cdot 、\vec{X}^{(N)} $と$\vec{Y}^{(1)}、\vec{Y}^{(2)} \cdot \cdot \cdot 、\vec{Y}^{(N)} $のようにN要素の列ベクトルで表す。
横に並べた行列を定義しておく。
\begin{eqnarray}
X &\equiv& \left( \begin{array}{cccc}
\vec{X}^{(1)} &\vec{X}^{(2)} & \cdot \cdot \cdot & \vec{X}^{(N)}
\end{array} \right)
\end{eqnarray} 2つに分けた多次元パラメーター同士の相関を見たい場合、それぞれの多次元パラメーターをスカラー量に変換し、N個のスカラー量データの相関を測れば良い。これが「正準相関分析」である。変換に用いる列ベクトルを$\vec{a}$として、
\begin{equation}
\vec{a}^\mathrm{T} X = \left( \begin{array}{cccc}
\vec{a}^\mathrm{T} \vec{X}^{(1)} &\vec{a}^\mathrm{T} \vec{X}^{(2)} & \cdot \cdot \cdot & \vec{a}^\mathrm{T} \vec{X}^{(N)}
\end{array} \right)
\end{equation} となる。各要素がスカラーである一次元のN点データとなっている。この変換に使う$\vec{a}$には最終的な相関が最大となるようなものを用いる。
相関係数
その相関の度合いを表す概念としては「相関係数」を用いる(cf 倉田著 入門統計解析p.72など)。2データ$x,y$の間の相関係数$\rho$は、共分散$S_{xy}$、標準偏差$S_x, S_y$、分散$\delta_x, \delta_y$などとすると、次のようになる。
\begin{eqnarray}
\rho &=& \frac{S_{xy}}{S_x S_y} \\
&=& \frac{S_{xy}}{\sqrt{\delta_x} \sqrt{\delta_y}} \\
&=& \frac{\vec{a}^\mathrm{T} V_{xy} \vec{b}} {\sqrt{\vec{a}^\mathrm{T} V_{xx} \vec{a}} \sqrt{\vec{b}^\mathrm{T} V_{yy} \vec{b}} }
\end{eqnarray}
Lagrangeの未定乗数法
相関係数$\rho$の表式は
\begin{eqnarray}
\rho &=& \frac{\vec{a}^\mathrm{T} V_{xy} \vec{b}} {\sqrt{\vec{a}^\mathrm{T} V_{xx} \vec{a}} \sqrt{\vec{b}^\mathrm{T} V_{yy} \vec{b}} }
\end{eqnarray} であった。これを最大にしたい。分子にある2項について、$\sqrt{\vec{a}^\mathrm{T} V_{xx} \vec{a}}=1, \sqrt{\vec{b}^\mathrm{T} V_{yy} \vec{b}} = 1$という条件を付けると、式がとても簡単になる。この条件下で$\rho$を最大化しよう($\vec a, \vec b$ は定数倍しても$\rho$は変化しないので制限を課しても問題ない)。Lagrangeの未定乗数法を用いる。
\begin{eqnarray}
L(\vec a, \vec b, \lambda_x, \lambda_y) &\equiv& \vec{a}^\mathrm{T} V_{xy} \vec{b} - \frac{\lambda_x}{2} (\vec{a}^\mathrm{T} V_{xx} \vec{a} -1) - \frac{\lambda_y}{2} (\vec{b}^\mathrm{T} V_{yy} \vec{b} - 1)
\end{eqnarray}として、偏微分を計算すると
\begin{eqnarray}
\frac{\partial L}{\partial \vec a} &=&
\left( \begin{array}{c}
\frac{\partial L}{\partial a_1} \\ \frac{\partial L}{\partial a_2} \\ \cdot \\ \cdot \\ \cdot \\ \frac{\partial L}{\partial a_N}
\end{array} \right) = V_{xy}\vec b - \lambda_x V_{xx} \vec{a} \\ \\
\frac{\partial L}{\partial \vec b} &=& V_{xy}^{\mathrm T} \vec a - \lambda_y V_{yy} \vec{b}
\end{eqnarray}
偏微分が0になることから、次の2式が導出される。
\begin{eqnarray} \left\{ \begin{array}{r@{\,}r@{\,}r}
V_{xy}\vec b - \lambda_x V_{xx} \vec{a} = 0 \\
V_{xy}^{\mathrm T} \vec a - \lambda_y V_{yy} \vec{b} = 0
\end{array} \right. \end{eqnarray} 第二式を変形して、
\begin{eqnarray}
\vec b = \frac{1}{\lambda_y} V_{yy}^{-1} V_{xy}^{\mathrm T} \vec a
\end{eqnarray} これを第一式に代入して、
\begin{eqnarray}
V_{xy} V_{yy}^{-1} V_{xy}^{\mathrm T} \vec a = \lambda_x \lambda_y V_{xx} \vec{a}
\end{eqnarray} 条件式は次の2式となった。
\begin{eqnarray} \left\{ \begin{array}{r@{\,}r@{\,}r}
V_{xy} V_{yy}^{-1} V_{xy}^{\mathrm T} \vec a &=& \lambda_x \lambda_y V_{xx} \vec{a} \\
\vec b &=& \frac{1}{\lambda_y} V_{yy}^{-1} V_{xy}^{\mathrm T} \vec a
\end{array} \right. \end{eqnarray}
Cholesky分解
Cholesky分解を行う。
\begin{eqnarray}
V_{xx} = L_{xx} L_{xx}^{\mathrm T}
\end{eqnarray} のように分解すると、
\begin{eqnarray}
V_{xy} V_{yy}^{-1} V_{xy}^{\mathrm T} \vec a &=& \lambda_x \lambda_y L_{xx} L_{xx}^{\mathrm T} \vec{a} \\
L_{xx}^{-1} V_{xy} V_{yy}^{-1} V_{xy}^{\mathrm T} (L_{xx}^{\mathrm T -1} L_{xx}^{\mathrm T}) \vec a &=& \lambda_x \lambda_y L_{xx}^{\mathrm T} \vec{a} \\
L_{xx}^{-1} V_{xy} V_{yy}^{-1} V_{xy}^{\mathrm T} L_{xx}^{\mathrm T -1} (L_{xx}^{\mathrm T} \vec a) &=& \lambda_x \lambda_y (L_{xx}^{\mathrm T} \vec{a})
\end{eqnarray} これで固有値問題へと帰着された!!
固有方程式を解くことで、$\vec a$が求まり、さらに「$\vec b = \frac{1}{\lambda_y} V_{yy}^{-1} V_{xy}^{\mathrm T} \vec a$」と「$\vec{b}^\mathrm{T} V_{yy} \vec{b} = 1$」を満たすような$\vec b$も求めることが出来る。$\vec a , \vec b$から、相関係数$\rho = \vec{a}^\mathrm{T} V_{xy} \vec{b} $が求まる。








